Помогите с решением задачи. На голову приходит только перебор за экспоненту…
Вот ссылка:
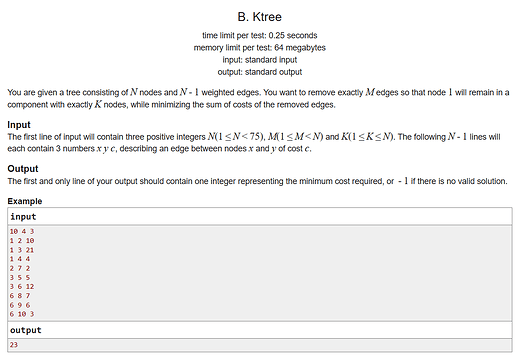
Задача - B - Codeforces
подсказка 1!
динамическое программирование
подсказка 2!
динамическое программирование по поддеревьям!
подсказка 3!
dp[i][j][k2], где i - текущая вершина где мы стоим и мы набрали j вершин в поддереве и убрали k2 ребер!
фулл решение!
dp[i][j][k2], где i - текущая вершина где мы стоим и мы набрали j вершин в поддереве и убрали k2 ребер!
Будем проходить дерево начиная с вершины 1 с помощью дфса.
Допустим мы стоим вы вершине v, то тогда можно сделать компоненты размера 1 из вершины v, dp[v][1][(колво ребер выходящих из v в сыновья)] = сумма цен этих ребер.
Это будет базой дпшки.
Теперь давай перебирать сыновья и текущее состояние дпшки, пусть будет dp[i][j][k2], то теперь давай рассмотрим ребро из v в son.
- Мы можем его убрать.
То тогда давай перебирать sz - размер компоненты son и reb сколько ребер было убрано в нем. То тогда переход такой:
dp[v][j][k2 + reb] = min(dp[v][j][k2 + reb], dp[v][j][k2] + cost), cost - (цена ребра) - Мы возьмем это ребро.
То тогда давай перебирать также sz - размер компоненты son и reb сколько ребер было убрано в нем. То тогда переход такой:
dp[v][j + sz][k2 + reb] = min(dp[v][j + sz][k2 + reb], dp[v][j][k2] + dp[son][sz][reb])
Ответ будет находиться в dp[1][k][m].
В общем решение грубо говоря будет работать за 10^8, а так как там тл 0.25 sec, то код может не зайти, но можно добавить некоторые оптимизации и еще codeforces довольно быстрый и оно должно зайти.