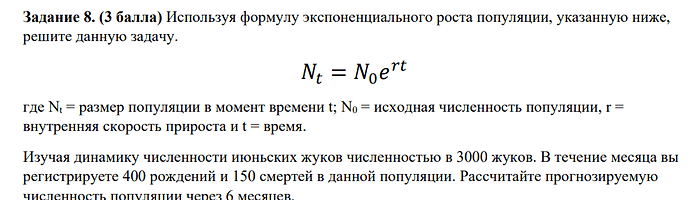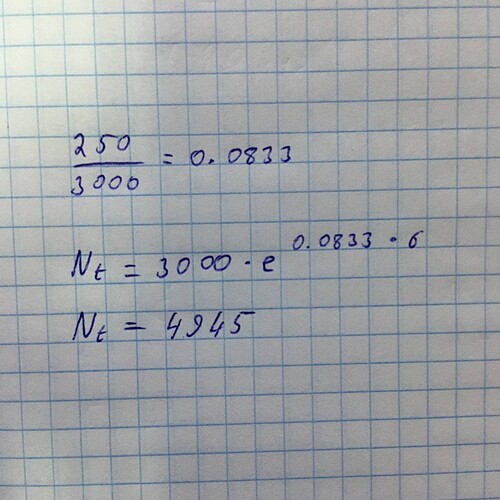В этой теме обсуждаем задачи national олимпиады 2021 года
Это обсуждение публикации https://olympiads.bc-pf.org/biology/national/2021/9
Это обсуждение публикации https://olympiads.bc-pf.org/biology/national/2021/9
Ошибки в решении не вижу.
По задаче, кстати, не совсем понятно от какой точки идет расчет 6 месяцев. С момента регистрации прироста? Или от начальной популяции 3000? Если второе, то ответ 4850. Если первое, то ответ ~5200
Думаю данный мой ответ плюс минус совпадает с ответом (зависит от того сколько чисел после запятой вы взяли при нахождении скорости прироста)
3 лайка
Это может быть официальным решением, но это точно не правильное решение.
Давайте сначала попытаемся понять какой физический смысл у скорости 250/3000=0.0833. Что мы имеем? В начале месяца мы имеем 3000 особей, в конце месяца 3250. 250/3000 можно интерпретировать двумя способами.
С одной стороны, мы можем сказать, что в начале месяца мы фиксируем кол-во жуков, которые способны умирать и размножаться. По мере протекания месяца, какие-то жуки будут умирать, какие-то жуки будут рождаться - но вот эти события не имеют влияния на кол-во жуков в конце. Условно говоря, жук, который родился третьего числа не сможет размножаться до конца месяца.
С другой стороны, мы можем сказать, что жуки могут размножаться и умирать в любой момент времени, т.е. жук, рожденный третьего числа (т.е. не существовавший на начало месяца) может родить еще одного жука к концу месяца. И тогда скорость размножения будет определяться не интервалом “месяц”, а чем-то короче. Например, неделя, день, час, минута, секунда, мгновение. Любая скорость, посчитанная на не бесконечно малом интервале, тогда, будет лишь средней скоростью. А мгновенная скорость определяется через производную dN/dt.
Если процесс подчиняется мгновенной скорости (т.е. каждый новый элемент может мгновенно претерпевать что-либо), то средняя скорость на равных по величине но разных по сущности интервалах зависит от размера этих величин.
Например. Возьмем экспоненциальный рост y=2^t.
| Время (t) | Кол-во (y) |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
Возьмем два равных по величине отрезка: t \in [1, 2] и t \in [3, 4]. Каждый отрезок имеет \Delta t=1. Сравним средние скорости \Delta y / \Delta t: для первого интервала 2, для второго интервала 8.
Таким образом, если мы допускаем, что жуки размножаются экспоненциально, то подсчет скорости размножения как средней скорости является лишь приближением, причем чудовищным грубым.
Поэтому, чтоб хоть как-то спасти официальное решение, мы должны допустить, что жук, рожденный после начала месяца не может умереть или родить еще кого-то.
Юмор
Определенный представитель насекомого появившийся в текущий отчетный период не может претерпевать процессы, характерные для иных представителей насекомых, существовавших в до начала текущего отчетного периода
Но тогда, в последующие 5 месяцев, мы должны придерживаться тех же самых допущений. Т.е. если на конец первого месяца у нас было 3250 жуков, а скорость прироста 0.0833, то к концу месяца прирост составит 0.0833\cdot 3250 \approx 271, и в конце второго месяца у нас будет 3250+271=3521 жук.
В общем виде, мы используем геометрическую прогрессию с расчетным периодом в месяц:
N_t = N_0 \cdot (1+250/3000)^6 \approx 4849.4657037680
Я не зря написал так много чисел после запятой. Ничего не замечаете?
Напомню:
r=\ln \frac{3250}{3000} \approx 0.080
N_t = N_0 e^{rt} = 3000 e^{6r} = 4849.4657037680
Атас! На самом деле, это просто совпадение. В данной задаче мы имеем дело с довольно маленькой скоростью роста (относительно начального размера популяции), что разница между ежемесячным расчетом и расчетом чаще, чем ежесекундно, ничтожна.
А все дело в том, что при достаточно маленьких значениях x, функция e^x может быть разложена в ряд Тейлора:
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \dots
И мы можем заметить, что первые два слагаемых мы уже где-то видели. Попробуем оценить размер третьего слагаемого для x=0.0800
\frac{0.08^2}{2} \approx 0.0032
Что, по сравнению с 1+x еле заметно (меньше 0.3%)
Короче, в любом случае, в данной задаче, вне зависимости от модели, мы получаем один и тот же ответ (отличный от официального). А официальный ответ является результатом смешения двух моделей: мы допускаем экспоненциальный рост, но скорость считаем как при ежемесячном росте. Скорость посчитали как при ежемесячном, но потом кол-во особей считаем как при экспоненциальном.
11 лайков