Dшка Юниорки 2021

Информатика
1

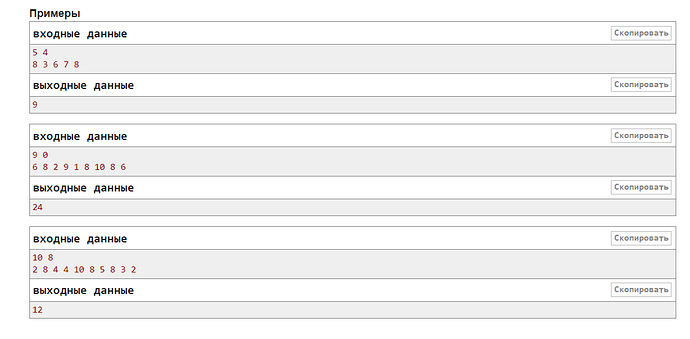
Как решить на 100 баллов? Удалось только сделать 1-3 подзадачи, до 4 не могу додуматься.

chrome_uKk7k3WwId
chrome_uKk7k3WwId1156×612 62.2 KB

chrome_Wcj57WW0WZ
chrome_Wcj57WW0WZ1152×567 17.6 KB

2

Так я не знаю это работает или нет. Кажется тут разделяйка.
То есть че:
давай запустим rec(l = 1, r = n).
и находить ответ теперь m = (l + r) / 2;
Давай посмотрим типа минимум, он жб будет где то либо в i <= x <= m или m + 1 <= j для отрезка (i, j). ну и давай допустим минимум в правой стороне то давай хранить префиксный минимум и теперь нужно найти такую границу l, что a[i] ^ a[l] == x и суффиксный минимум от m до l должен быть больше или равен минимуму на этом префиксе. Вроде бы так решается для правой стороны и тоже самое для левой.

3 лайка
3

понял?

1 лайк
4

да, понял

5

У @Nursik неплохое решение, однако для тех кто ненавидит разделяйку и непонятный код есть решение в разы красивее (и медленнее в log раз, которое все равно комфортно заходит (а еще оно вообще авторское)).

Начнем с интересного факта:

Если предпосчитать для каждого элемента на позиции i самые близкие левые / правые границы (l[i],r[i]), такие что min(a[j])_{j \in [l[i] - 1, i]} < a[i], и min(a[j])_{j \in [i, r[i] + 1]} \leq a[i], то пройдясь циклом по более короткому отрезку из (l[i], i) и (i, r[i]) мы суммарно совершим O(nlogn) операций.

Доказывать его я, разумеется, не буду, но в разборе задачи E на CF все довольно понятно описано.
Что нам это дает?
Обозначим “левой частью” (l[i], i), а “правой частью” (i, r[i]). Для удобства будем решать задачу для конкретных a[i], которые мы зафиксируем как минимум на отрезке благодаря уже предпосчитанным l[i] и r[i], и еще для удобства примем, что левая часть - меньшая по длине, потому что иначе все симметрично.
Наше условие корректности отрезка - a[l] ^ a[r] = x, тогда ясно, что перебирая циклом a[j] в левой части (то есть j \in [l[i], i]), нам нужны a[k] = a[j] ^ x в правой части (то есть k \in [i, r[i]]), причем нам нужно максимизировать (r - l + 1), поэтому просто найдем бинпоиском самый правый a[k], который все еще лежит в правой части и обновим ответ значением a[i] * (k - j + 1).
Поскольку мы уже доказали, что проход по таким необычным границам, которые заданы l[i] и r[i] суммарно занимает O(nlogn) операций, и поскольку поверх этого мы делаем бинпоиск, то суммарно все будет работать за O(nlog^2n)

Код 
ll n, x, k, a[200005], l[200005], r[200005];
vector<ll> v;
set<ll> p[200005];
int main() {
  speed;
  precision;
  // code
  cin >> n >> x;
  for (int i = 1; i <= n; i++) {
    cin >> a[i];
    p[a[i]].insert(i);
    while (sz(v) && a[i] <= a[v.back()]) v.pop_back();
    l[i] = (sz(v) ? v.back() : 0) + 1;
    v.pb(i);
  }
  v.clear();
  for (int i = n; i >= 1; i--) {
    while (sz(v) && a[i] < a[v.back()]) v.pop_back();
    r[i] = (sz(v) ? v.back() : n + 1) - 1;
    v.pb(i);
  }
  for (int i = 1; i <= n; i++) {
    if (i - l[i] < r[i] - i) {
      for (int j = l[i]; j <= i; j++) {
        if (!sz(p[a[j] ^ x])) continue;
        auto it = p[a[j] ^ x].upper_bound(r[i]);
        if (it == p[a[j] ^ x].begin()) continue;
        it--;
        if (*it < i) continue;
        k = max(k, a[i] * (*it - j + 1));
      }
    } else {
      for (int j = i; j <= r[i]; j++) {
        if (!sz(p[a[j] ^ x])) continue;
        auto it = p[a[j] ^ x].lower_bound(l[i]);
        if (it == p[a[j] ^ x].end() || *it > i) continue;
        k = max(k, a[i] * (j - *it + 1));
      }
    }
  }
5 лайков
6

Разделяй и властвуй? где можно его изучить.

7

так это просто идея по идее, что ты разделяешь отрезок на две части и отдельно считаешь на двух частях и считаешь что то и делаешь то же самое на этом отрезке.
и еще тут блог Applications of Divide and Conquer | Yet Another Competitive Programming Blog
или можешь найти другие написав: divide and conquer codeforces

1 лайк
8

Можно ссылку на задачу?

1 лайк
9

Лови!

1 лайк