Мое решение не очень то простое и быстрое, но лучшего пока нет)
Использовал я только эту формулу:
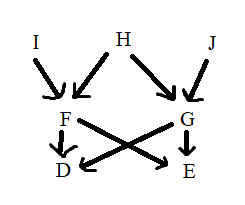
Итак, у нас есть генеалогическое дерево и лучше всего его представить в немного другом виде:
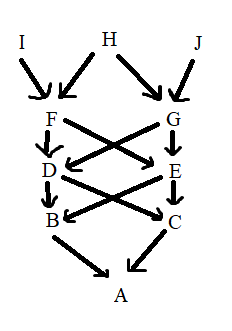
Каждая стрелка это просто передача генетической информации. И тут важно упомянуть что вообще значит коэффициент инбридинга(F) - это вероятность того, что у особи будет два одинаковых аллеля на одном из локусов, которые при этом были получены от предка. Теперь опять к формуле, она отдельно для каждого пути инбридинга и в конце значения каждого пути суммируются. Под путями я имею ввиду это:
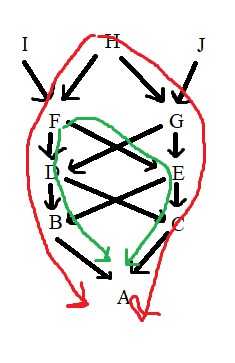
n - количество особей в каждом таком пути, не считая самого нижнего (A).
Fa - коэффициент инбридинга общего предка каждого пути (в зеленом пути предком будет F).
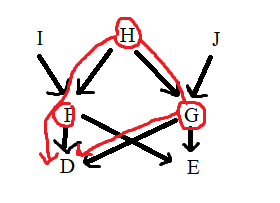
Нужно посчитать количество путей каждого вида предка (я покажу только пару ибо их слишком много, но в условии дана подсказка, что всего этих путей должно быть девять!!!):
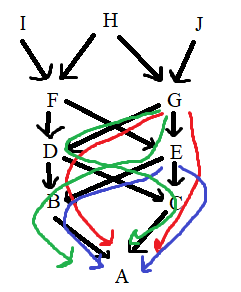
Смотрите из G выходит 2 пути, из E один, тоже самое мы можем симметрично сказать про F и D. Если 6 путей уже есть то оставшиеся три должны быть у H (опять же чтобы было девять в сумме). И еще один момент перед тем как можно будет начинать считать - у D и Е тоже есть какой-то уровень инбридинга(1/8 если быть точнее), это можно посчитать если использовать только верхнюю часть схемы.
Для путей Е и D:
Для путей F и G:
И для H:
Сумма всего этого = 0,4297
а как посчитать коэфициент инбридинга предка?(Fa)
Посмотри на этот фрагмент, он уже довольно простой.
Для D и E всего по одному пути:
n = 3, путь один, поэтому:
Точно так же для Е