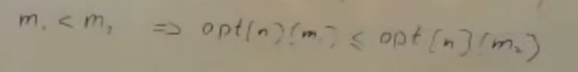
Можете объяснить почему выражение с opt является верным?
Задача. Даны n точек на прямой, отсортированные по своей координате. Нужно найти m отрезков, покрывающих все точки, минимизировав при этом сумму квадратов их длин.
Оптимизация через разделяй-и-властвуй - Алгоритмика - идея такая же как и здесь но формула идея opt отличается
Как ты определяешь opt[n][m]?
Допустим ты имеешь ввиду оптимальный переход для покрытия первых m точек n отрезками, тогда:
(Для удобства $k_1 = opt[n][m_1], k_2 = opt[n][m_2])
Скажем что k_1 точно посчитано правильно.
Допустим то что k_2 (k_2 < k_1) реально оптимальная точка.
dp[n][m_2] = dp[n - 1][k_2] + (point[m_2] - point[k_2])^2
Тогда
dp[n - 1][k_2] + (point[m_2] - point[k_2])^2 \leq dp[n - 1][k_1] + (point[m_2] - point[k_1])^2 | (1)
dp[n - 1][k_1] + (point[m_1] - point[k_1])^2 < dp[n - 1][k_2] + (point[m_1] - point[k_2])^2 | (2)
(Скажем что оптимальную точку самую левую выбираем для удобства, из этого следует строгость неравенства выше)
(1) \implies dp[n - 1][k_2] + (point[m_1] - point[k_1])^2 \leq dp[n - 1][k_1] + (point[m_2] - point[k_1])^2 + (point[m_1] - point[k_1])^2 - (point[m_2] - point[k_2])^2 | (3)
(2) and (3) \implies dp[n - 1][k_1] + (point[m_1] - point[k_1])^2 < dp[n - 1][k_2] + (point[m_1] - point[k_1])^2 \leq dp[n - 1][k_1] + (point[m_2] - point[k_1])^2 + (point[m_1] - point[k_1])^2 - (point[m_2] - point[k_2])^2
\implies dp[n - 1][k_1] + (point[m_1] - point[k_1])^2 < dp[n - 1][k_1] + (point[m_2] - point[k_1])^2 + (point[m_1] - point[k_1])^2 - (point[m_2] - point[k_2])^2
\implies (point[m_1] - point[k_1])^2 < (point[m_2] - point[k_1])^2 + (point[m_1] - point[k_1])^2 - (point[m_2] - point[k_2])^2
\implies (point[m_2] - point[k_2])^2 < (point[m_2] - point[k_1])^2
Но k_2 < k_1 \leq m_2 \implies point[k_2] \leq point[k_1] \leq point[m_2]
\implies (point[m_2] - point[k_2])^2 \geq (point[m_2] - point[k_1])^2
Противоречие, значит допущение не верно (я про (1)), то есть k_2 это не оптимальная точка, следовательно не может быть что k_2 < k_1, если k_1 это opt[n][m_1].
Дальше чтобы закончить пруф что неравенство с opt выполняется везде нужно просто сделать индукцию.
Хороший пруф, но мне кажется, что он очень недружелюбный для начинающих (ну я например где-то на середине забил читать). Есть ли какой-то более интуитивный способ понять что это правда и как выглядят задачи с D&C оптимизацией?
Я например никогда твердо не понимал почему эта оптимизация работает, и задач на нее мало, ну просто примерная чуйка и обычно до нее доходишь только если хз чё писать и перебираешь варианты.
В дп с блоками вариантов что делать не прям много.
Логика обычно в том что у тебя оптимальная точка перехода для более правых состояний всегда правее, и ты делаешь почти тоже самое что и в
параллельном бинарном поиске.
Чтобы алгоритм работал нужно чтобы точки оптимальных переходов не убывали