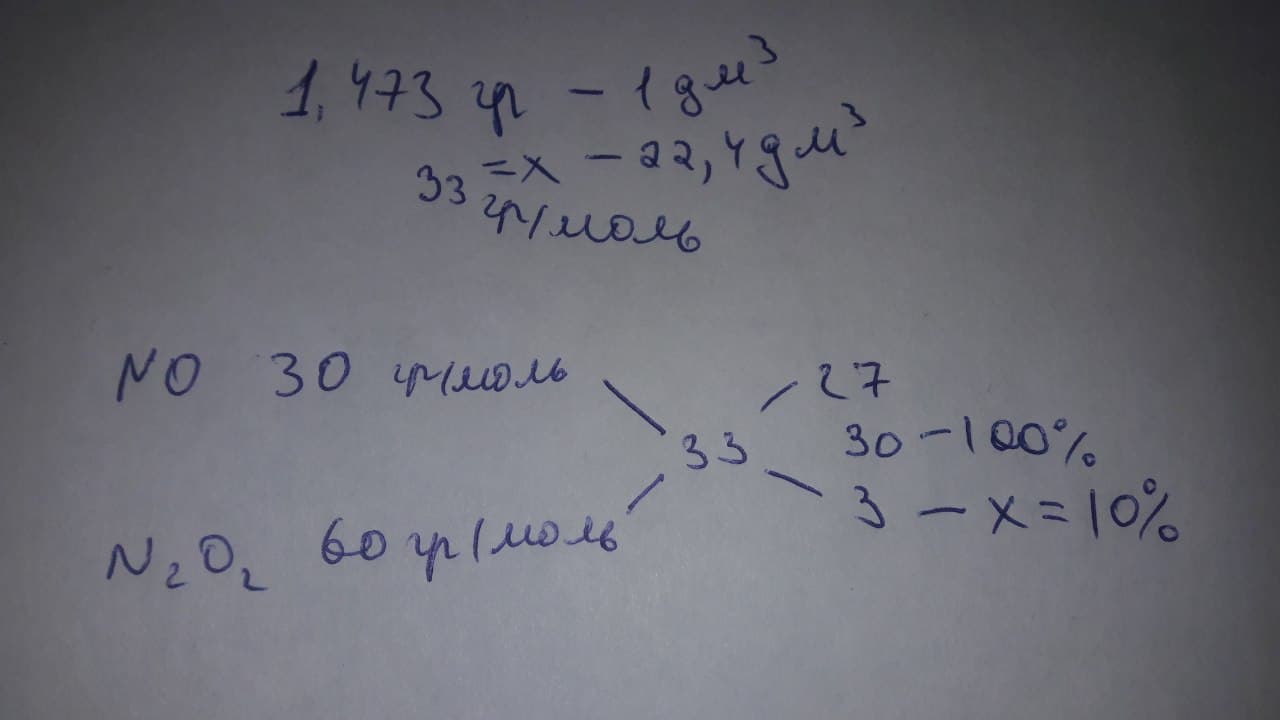В газообразном состоянии молекулы \ce{NO} частично димерозованы.При некоторой температуре плотность смеси ,состоящей из \ce{NO,N2O2} равна 1,473 г/дм3.Найдите обьемную долю \ce{N2O2} в такой смеси.
Для начало у тебя был газообразный NO, потом молекулы NO начали димерозоваться
2 NO \to N_2O_2
n_{начальное}(NO) = x
n_{прореогировало}(NO) = y
то n_{образовавшегося}(N_2O_2) = 0.5y
d_{смеси} = \frac{m_{смеси}}{v_{смеси}}=\frac{(x-y)*30+30y}{((x-y) + 0.5y)*22.4} = 1.473
решая это у нас выходит 5.508y = x
то мольная доля N_2O_2 = 9.984%
Почему ты взял как 22,4? Это же не факт что 1 моль равен 22.4л, тут неопределённая температура, то есть возможно здесь не нормальные условии
Самый легкий способ для решения именно задач этого уровня это взять что условия стандартные то есть V_m = 22,4
в этом случае они были дали точные данные, сказав что температура такая то, и давление такое…
Придётся взять как 22.4л, так как температура, давления не даны. А так ты прав, там не сказано что там нормальные условия
ну стоит заметить, что если прореагировало y моль NO, то образовалось 0.5у моль димера.
сори опечатка, изменил
Немного другой способ решения. Если за \alpha обозначить объемную долю \ce{NO} и принять, что газы идеальные, будет справедливо следующее:
Отсюда видно, что информации в задаче недостаточно. Но если будет известен молярный объем, можно решить задачу. При нормальных условиях ответ совпадает с тем, что дал @kourai.
Ну раз в задаче отметили, что “некоторая температура”, здесь (да и вообще, всегда) стоило бы указать условия. Если условия далеки от нормальных, в идеале еще сказать, можно ли принять газы идеальными.
Падажжите, товарищи!
Нам все таки нужно найти объемную долю, так? Надо попробовать решить задачу с произвольной V_m потому что может быть такое, что при делении одного объема на другой, эта V_m сократится.
Я попробую чуть позже, но может кто опередит меня
Я пробовал, правда долго не сидел, может чего-то не увидел. Но кажется, что ничего не будет сокращаться, потому что конкретное значение V_\text{m} определяет конкретное значение молярной массы смеси. Зависимость молярной массы смеси от мольной доли одного из компонентов линейная, а значит монотонная, а значит каждое значение принимает всего раз. То есть, нет такого значения \alpha, которое могло бы подходить под два разных значения V_\text{m}. А тогда про произвольное и речи быть не может. Ну если я где-то не ошибся.
А, ой, точно, да, уравнение с двумя неизвестными
Кстати, у меня одного другое значение:
(30(x-y)+30y)/((x-y+0.5y)*a)=1.473; z=y/(x+y); a=22.4
Вольфрам дает 15.37\%
3-й способ решения
как я понял z это доля, там же 0,5y/x-0,5y должно быть тогда