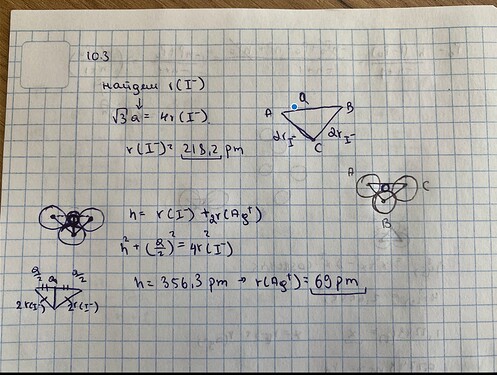У меня получилось ровно 63.5 пм (при условии, что у меня r(\ce{I-})= 218.24 \ пм.
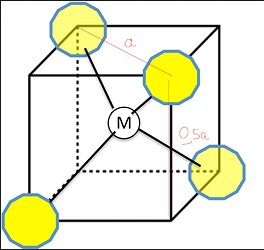
Думаю тебе не сложно найти радиус \ce{I-}, ибо ее можно найти по простой формуле r=\frac{\sqrt 3}{4}a, которую можно вывести чисто с помощью теоремы Пифагора. Далее, судя по условию, ионы серебра находятся как раз таки в октаэдрических, или тетраэдрических пустотах. Также, по условию, ионы серебра свободно могут перемещаться из октаэдрической пустоты в тетраэдрическую, и наоборот.
Попробуем найти максимальные радиусы ионов серебра в октаэдрическом и тетраэдрическом пустотах.
-
Октаэдрическая пустота
Видно, что длина диагонали плоского квадрата, построенного из иодид аниона равна 2r(\ce{I-})+2r(\ce{Ag+}). А эту длину диагонали можно найти по теореме Пифагора, и тогда получается, что 2r(\ce{I-})+2r(\ce{Ag+}) = (504^{2} +504^{2})^{0.5} , и отсюда r(\ce{Ag+)} = 138.14 \ пм -
Тетраэдрическая пустота
Здесь немного неочевидно, но можно облегчить задачу, если построить куб, на 1/2 вершинах которого находятся иодид ионы
Отсюда можно заметить, что длина диагонали куба это по сути 2r(\ce{I-}) + 2r(\ce{Ag+}), а эта длина равна (a^{2} + (0.5a)^{2})^{0.5} = 1.118a. Т.е получается, что r(\ce{Ag+}) = 63.5 \ пм.
И тут, казалось бы, очевидно что ответом должен быть 138 пм (ну типа максимум). Однако, вся соль заключается в том, что
ионы серебра свободно могут перемещаться из октаэдрической пустоты в тетраэдрическую, и наоборот
Это означает, что если бы радиус ионов серебра был равен 138 пм, то ионы серебра попросту не могли бы свободно перемещаться из одной пустоты в другую именно под действием электрического поля. Следовательно, максимальный радиус ионов серебра должен быть равен 63.5 пм
Благодарю
У меня другой вариант: Если рассмотреть куб, который нарисовал @Madsoul, то можно найти радиус серебра через теорему косинусов. Возьмем верхний треугольник, где одна сторона равна a, противоположный угол равен 109.5, а две другие стороны x
Из рисунка видно, что x это сумма радиусов серебра и йода, тогда r(Ag^+)=80 пм.
В итоге несостыковочка.