Из заданных параметров волны \lambda и T очевидным образом находится скорость распространения волн:
c = \lambda/T.
Далее рассмотри тот момент времени, когда катер находился на неизвестном расстоянии x от точки B (ну или угол \alpha между AB и направлением на катер), причём в этот момент от катера появляется гребень волны, который первым ударит точку A. Геометрия довольно ясна, но появляется вопрос: какое условие нужно задать для того, чтобы именно в этот момент появлялся первый гребень?
Спойлер
Проекция скорости катера на направление волны в этот момент равна самой скорости волны, или же v\sin \alpha = c.
3 лайка
а тут время t это же не \frac{L}{c*cos(\alpha)} , а это минус \frac{L ctg(\alpha)}{V} ?
время t отсчитывается уже после того, как катер пересечёт точку B, так что внимательно проследи за положениями катера и распространением гребни волны
окей я получил правильный ответ, но могли ли мы вывести это условие из соображений что время для первой волны минимальна? и вообще как мы так сразу сказали условие ?
суть в том, что если угол \alpha слишком большой (что даёт нам неравенство v \sin \alpha > c), то гребни волны в направлении точки A хоть и образовываются, но из-за движения лодки всё ещё могут появляться те гребни, что достигнут точки A всё-таки раньше, чем предыдущие волны.
ну а как получить условие?
можно, конечно, и через принцип Ферма, но на таких олимпиадах, как мош, такой матанализ и не нужен особо. Всё же покажу решение:
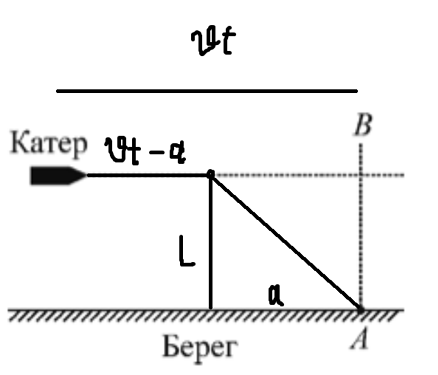
Определим какое-нибудь положение катера, причём его расстояние до точки B равно vt (t<0, а когда катер в точке B, то t=0). Тогда для того, чтобы с этого момента волна достигла точки A, катер проплывёт до тех пор, пока расстояние до B не будет равно какому-то произвольному a, а затем этот гребень будет распространяться по диагонали от той точки. Время, которое тратит волна на это, равно
\tau = \frac{vt-a}{v} + \frac{\sqrt{L^2+a^2}}{c}.
Для первой волны, достигшей точки A, это время минимально, значит \displaystyle \frac{\partial \tau}{\partial a} = 0, ну или
\frac{\partial \tau}{\partial a}=-\frac{1}{v} + \frac{1}{c}\frac{a}{\sqrt{L^2+a^2}}=0
А так как \displaystyle \sin \alpha = \frac{a}{\sqrt{L^2+a^2}}, то мы получаем то условие, которое я написал выше.
2 лайка
вово, я также предлагал делать, теперь уже все понятно, спасибо!