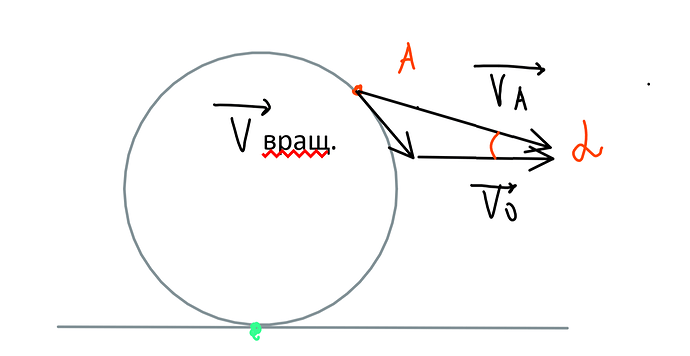
Скажите пожалуйста, Я вообще правильно рассуждаю или нет, а то у меня ответ(на первый вопрос) вообще не схож с тем, что есть в учебнике(
Вот мои каракули:
1 лайк
Сначала запиши координаты точки в полярных координатах:
x=R\sin\varphi+v_0t, y=R\cos\varphi
Чтобы найти скорости найди производные координат:
\dot x=\dot \varphi R\cos\varphi+v_0, \dot y=-\dot \varphi R\sin \varphi
Посмотрим что написано в указании:
Отсюда ясно, что:
v_0=\dot \varphi R \Rightarrow \dot x=v_0(1+\cos\varphi), \dot y=-v_0\sin \varphi
Полная скорость точки:
v_A=\sqrt{\dot x^2+\dot y^2}=v_0\sqrt{2(1+\cos\varphi)}
Учитывая:
\cos^2 \frac{\varphi}{2}=\frac{1+\cos \varphi}{2}\Rightarrow v_A=2v_0\cos \frac{\varphi}{2}
Угол \alpha между вектором полной скорости и направлением поступательного движения его центра находится через треугольник, получающийся векторным сложением скоростей:
\vec v_A=\vec v_0+\vec v_{вращ.}
Из указания выше:
v_0=v_{вращ.}=\dot \varphi R
В результате получается равнобедренный треугольник, для которого справедливо равенство:
2v_0\cos \alpha=v_A=2v_0\cos\frac{\varphi}{2}\Rightarrow \cos \alpha =\cos \frac{\varphi}{2}\Rightarrow \alpha=\frac{\varphi}{2}
6 лайков