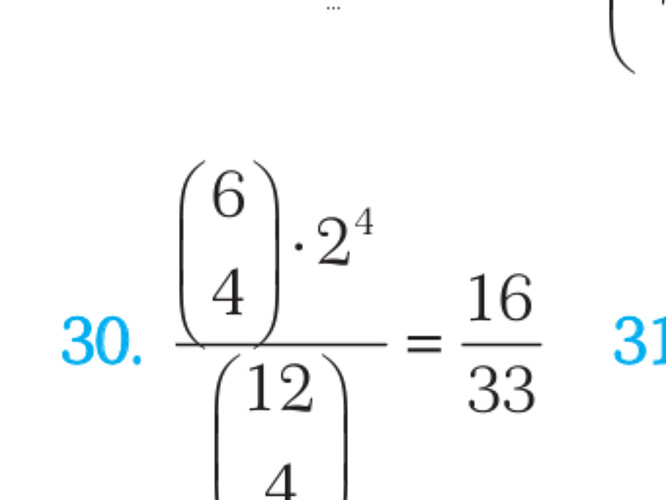A group of 4 people is chosen at random from 6 couples. What is the probability that there is no couple in the group?
Можете объяснить решение. Я понял откуда вышел знаменатель в дроби (у нас общая количества комбинации 12С4). Но не совсем понятно откуда вышли верхние числа.
Мне тоже стало интересно. Лично я попробовал как-то проще (имхо) найти число комбинации, в которых нет пар. На первом месте может быть 12 людей, на втором месте может быть 10 людей (потому что 1 человек находится в паре), на третьем месте может быть 8 людей, а на четвертом месте может быть 6 людей (по той же причине). Всего получится 12 * 10 * 8 * 6 = 5760 вариантов. Поскольку нам порядок вообще не важен, то надо соответственно поделить это число на 4!, и тогда мы получим число комбинации таких групп, в которых нет пар. Отсюда и 5760 / 4! = 240, и далее, вероятность = 240 / 495 = 16/33 (возможно, я имплицитно сделал то же самое, что и в решении этой задачи, но не совсем уверен)
Спасибо. Я все понял
В авторском решении предложили перебрать те пары, из которой один человек будет находиться в группе, это и есть 6C4. Когда мы знаем из каких групп мы выбираем человека осталось посчитать количество способов выбрать этих самых людей, в каждой из четырех групп у нас два варианта, отсюда мы и умножаем на 2^4.