Лестница длиной L приставлена к гладкой стене под углом к полу 60°. Максимальная сила трения между лестницей и полом 200H. На какую максимальную высоту может подняться по лестнице человек массой m, прежде чем лестница начнет скользить? Массой лестницы пренебречь.
1 лайк
У тебя уже есть какие-то наработки или идеи как решать задачу? Или ты не можешь начать решение?
Да, не могу никак составить моменты сил
Что удобно в моментах сил, особенно при работе с неподвижными объектами: можно взять любую ось и относительно неё моменты сил будут равны нулю. Поэтому всегда есть точки, относительно которых один или несколько моментов сил равны нулю.
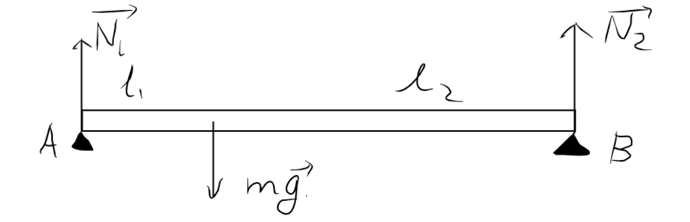
Математики любят сначала объяснять упрощенную задачу, а потом уже работать с полной версией. В физике такой метод тоже полезен, поэтому полезно рассмотреть сначала задачу попроще. Есть неоднородная палка, центр масс которой делит её длину в отношении l_1 / l_2, и её концы установили на две опоры (см. рисунок). Нужно найти силы, с которыми опоры действуют на палку.
У этой задачи есть два метода: только через моменты; через моменты и закон Ньютона. Ключевая вещь в методе через моменты сил – найти ось так, чтобы было одно уравнение и одно неизвестное.
Метод через моменты
Если немного подумать и расписать разные точки, то можно прийти к выводу, что оптимальными будут точки, в которых находятся опоры:
- Относительное точки A:
mg*l_1 = N_2* (l_1 + l_2)
- Относительное точки B:
mg*l_2 = N_2* (l_1 + l_2)
Вот так вот просто решается задача через моменты сил. В решении с использованием закона Ньютона центр масс выбран как ось для моментов сил. Он оставлен читателю в качестве самостоятельного упражнения
Теперь посмотрим на систему из основной задачи (m – масса человека):
Как видно, если взять точку О, то тогда момент сил N_1 и N_2 равен нулю и дальше задача решается очень просто через одно уравнение для моментов и два уравнения для первого закона Ньютона
6 лайков