Веревку, перекинутую через гладкий гвоздь, протаскивают со скоростью v сквозь щель. Сила трения в щели F, масса единицы длины веревки ρ.
Определите силу, действующую на гвоздь, если участки веревки по разные стороны гвоздя образуют угол α. При какой скорости веревка отойдет от гвоздя?
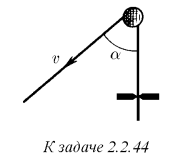
Помогите решить
чтобы веревка отцепилась нудно чтобы сила деиствующая на гвоздь юбыла равна нулю, сила от трения
[F`= 2F cos(a/2)]
сила от изменения импульса веревеки равна
[
F`` = 2mv cos(a/2)* p *v ]
[
F[res] = F` - F`` = 0
]
5 лайков
А как у вас вышел косинус половинного угла?
1 лайк
если не ошибаюсь то здесь нужно просто взять dm=pdL кусочек веревки и силы на него
1 лайк
Изобразим силы действующие на гвоздь. v=const, a=0 сила с которой тянут веревку равна силе трения F=F_{тр} . Из треугольника выходит что вектор от силы F’ направлено под углом \alpha /2 к каждому этих сил.
1 лайк
для F`, силы направлены в доль нити между ними угол a. На илюстраций представь F2 = F1, тогда
F’ = Fsqrt(2(1+cos(a)) = 2F cos(a/2)
Для F’’ представь дольку массы которая вот-вот подоидет г гвоздю dm = p dL , какую и в каком направлений нужно передать ему импульс чтобы он отклонился на угол 180 - a ?
формула будет такая же как для сил только в фомуле для сил использовалось теорема косинусов как ты мог заметить только наш угол находится в угле отклонения то-есть в левом верхнем углу, если мы представим для импульсов , поэтому в формулу подставь угол a.
Импульс dm . dP = v * dm= v* p* dL= v* p* v * dt
dP’’ = 2P cos(a/2)
F’’ = dP``/ dt = 2* p* v^2 * cos(a/2)
6 лайков