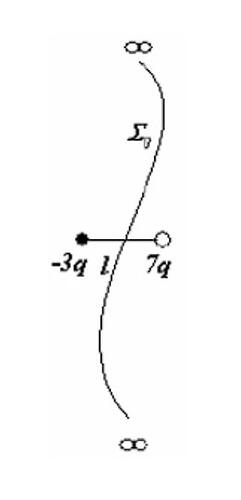
It is -3q in the second line.
Is the answer \Phi_0=\displaystyle\frac{5q}{\varepsilon_0}?
1 лайк
Oh I don’t have official key that’s why I asked here, could you send your method as well?
Well, on second thought, it was an answer to only a particular case. For example,
- Surface is an infinite plane. Then the flux from each charge equals half of their full flux, so \Phi_0 =\frac{(7q-(-3q))/2}{\varepsilon_0}=\frac{5q}{\varepsilon_0}.
- The surface is hyperbolic. Then the solid angles that cover the whole surface from respective charges are \Omega_1 and \Omega_2, and \Omega_1+\Omega_2=4\pi, so \Phi_0=(7q\Omega_1+3q\Omega_2)/(4\pi\varepsilon_0). The answer depends on how the surface diverges at infinity.
- The surface is parabolic or at least doesn’t diverge infinitely when it stretches to infinity (for example, it becomes cylindrical). Then the answer is either \Phi_0=7q/\varepsilon_0 or \Phi_0=3q/\varepsilon_0, depending on which charge it covers.
- The surface approaches the plane at infinity, but this asymptotic plane touches the line l outside the charges (hope you understand me). Then, for one of the charges, the flux is half the total flux of the charge, but for the second charge, it corresponds to the solid angle \Omega\leq2\pi.
6 лайков
It’s still hard to find out the exact answer because we don’t exactly know how the shape of the surface behaves at infinity
2 лайка
oh well only this was given in the problem…
1 лайк