Тут сперва надо найти напряженность полусфер с помощью теоремы Гаусса.Дальше находим силы с помощью формулы F=q×E
Мое утверждение правильное?
как бы ты применил теорему гаусса?
Наверное E×2πR²=Q/e0
поток надо высчитывать по замкнутой поверхности) тут конфигурация очень сложна, так что теорема гаусса тут бессмысленна. подумай о другом способе решить
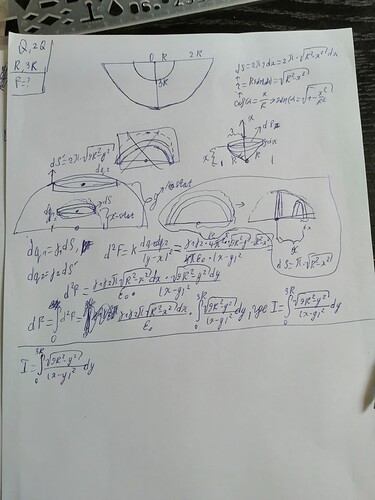
Алишер, у меня вроде норм решение(а может и нет, я сомневаюсь), но нужно решить сложный, по моему мнению, интеграл. Я его сейчас скину
Здесь, я взял и разделил малую окружность на кольцо(справа сверху), далее разделил большую окружность на кольца. Теперь рассматриваю силу d^2F, между двумя этими мини кольцами. Затем идёт интеграл
Для первой окружности придумал переменную x, для второй y. Для второй окружности принял, что x статично
ты перегнул) я и сам не помню решения этой задачи, но там не так сложно вроде бы
Да, нет) там нужно решить два интеграла и всё выйдет. Либо можно придумать какую-то хитрость.
А и, γ1 и γ2 - линейная плотность
Начало решения такое:
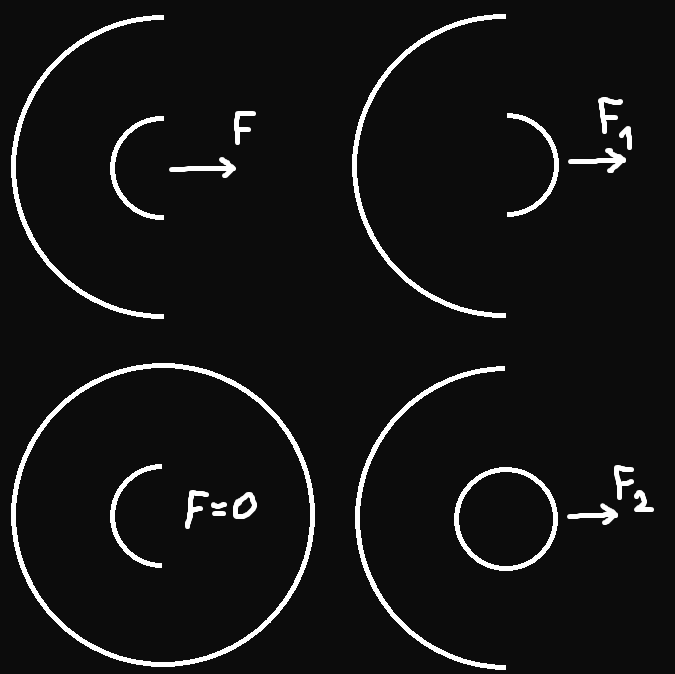
Cоотношение между F, F_1 и F_2 находится по этим рисункам, F_2 можно высчитать вручную.
