Постройте изображение предмета AB:
Есть идея поднять предмет и найти его изображение, затем провести перпендикуляры к г.о.о. или к какому-ту лучу. Чтобы уже получить изображение А’ и B’
Ну в первом случае, как-то сложно нарисовать сходу, поэтому подойдём к задаче численно, и подставим значения в формулу: \frac 1a + \frac 1b = \frac 1F
Для А
\frac 1F + \frac 1b = \frac 1f
\frac 1b равно нулю, только если b = \infty, то есть изображение точки а лежит на бесконечности.
Для В
Для В
\frac 10 + \frac 1b = \frac 1F
Получается бессмыслица, поэтому прибегнем к одному из распространённых принципов физики. Расстояние от B до линзы равно \delta \ll F.
\frac 1\delta + \frac 1b = \frac 1F\\
b = \frac {F\delta}{\delta - F} = - \frac {\delta}{1 - \frac \delta F}
Если обозначить x = \frac \delta F , то тогда, можно разложить знаменатель в ряд Тейлора:
\frac {1}{1 - x} \approx 1 + x
(Члены степенью большей 2 не имеет большого смысла рассматривать, так как \delta и так маленькое, а если возводить его в натуральную степень, то получится ещё меньше)
И тогда:
b \approx - \delta \left(1 + \frac \delta F\right) = - \delta - \frac {\delta^2}{F} = - \delta
Вернёмся к физике и вспомним, что означает отрицательное расстояние до изображения оно находится слева от линзы, а не справа
Предлагаю вам самим доказать, что изображения точек A и B находятся на таком же расстоянии от ГОО, как и сами точки A и B
Второе изображение строится аналогичным образом
5 лайков
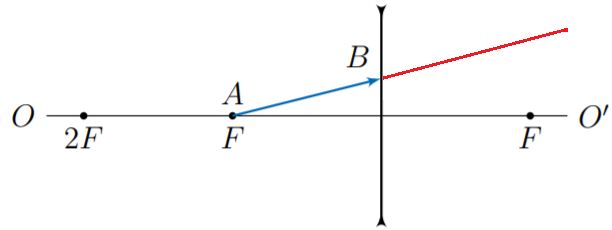
Как я понял, вот так?
