Добро пожаловать на форум! Пока что дам пару подсказок, вместо всего решения
-
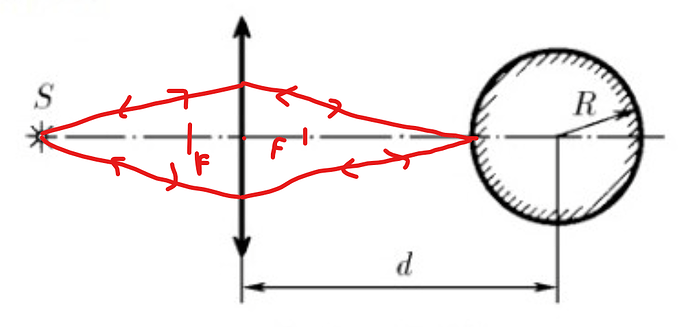
После того как получилось изображение источника в собирающей линзе, его можно использовать как сам источник для зеркального шарика
-
Зеркальный шарик можно считать сферическим зеркалом, что есть по сути собирающая линза, но преломленные лучи становятся мнимыми лучами, а продолжения преломленных лучей — видимые лучи
Пожалуйста,можете дать ещё подсказку.
Конечно могу)
Подсказка:
Нужно рассмотреть несколько случаев, где расстояния f, d, R как-то связаны ![]()
Ещё больше подсказка, которая реально что-то даёт
Рассмотрим один из случаев: d > R+f:
Расстояние от линзы, до первого изображения:
И так как это оптическая оптика в Савченко и про точность ничего не говориться, мы можем использовать классические пренебрежения оптической оптики: раствор лучей d \approx 0, то есть можно пренебречь всякими сферическими аберациями и кривизной шара (аналогично фразе “растворить (распахнуть) окно, чтобы проветрить комнату”, а не “растворить соль в этиловом спирте”, дорогие любители химии). Тогда можно написать
Далее делаем то же самое, что и парой абзацев выше, но уже для сферического выпуклого зеркала.
Страшилка
У меня там вышло кубическое уравнение, на которое смотреть страшно, не то, что решать
Мне только что подсказали гениальное и суперэлегантное решение этой задачи чисто через построения.
Чтобы изображение оказалось там, где находится источник, лучи должны вернуться так как ушли.
В случае, когда d > R + f, так произошло, есть два случая
Первый случай
- Первый, когда изображение выходит аккурат на поверхности сферы и тогда, можно считать, что оно отражается от плоского зеркала
Есть ещё два случая f< d< R + f и d< f
Предлагаю дальше самому подумать, порисовать над ними
Вывод.
Всегда стоит помнить, что у задач на оптику есть 2 решения:
- Через рисунки
- Через формулы
И прежде чем добивать один из способов, стоит чуточку времени уделить другому и посмотреть, что же легче
Спасибо,решил