Какая формула шестиугольника(кристаллические решетки) его объем куба , шарика и альфы?
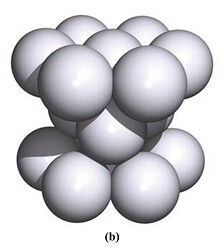
Я так понял, ты спрашиваешь о гексагональной решетке. Сначала посмотрим на то, как выглядит сама решетка (картинку взял из этой книги на 174 стр.):
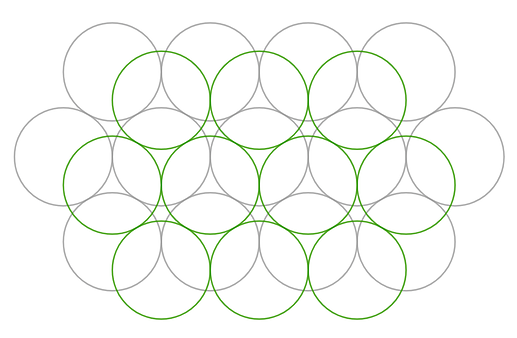
Если посмотреть сверху, это выглядит так:
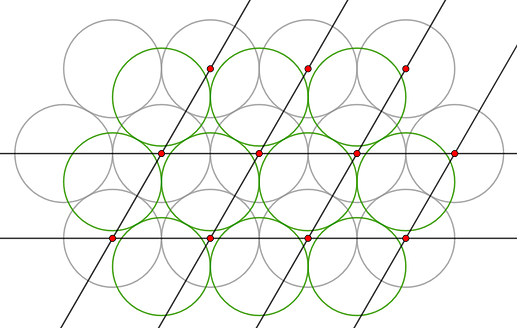
Наша задача — найти часть всей решетки, которая повторяется. В этом примере будем считать, что серые шары снизу, а зеленые — сверху. Через центры серых шаров можно провести прямые, из которых можно всю структуру поделить на кучу ромбиков:
Представим, что перед нами три уровня решетки. Самые верхние шары совпадают с самыми нижними. Мы можем с каждого центра нижних шаров провести прямые ровно вверх до центров самых верхних шаров (придется поднапрячь воображение). Тогда у нас получатся куча таких прямых призм.
Если мы захотим найти плотность решетки, мы можем просто найти плотность в одной из таких призм. Объем призмы — это площадь ее основания (в данном случае ромб), умноженная на ее высоту. Площадь ромба можно найти, разделив ромб на два равносторонних треугольника; для этого надо провести вторую диагональ ромба. Обозначим сторону ромба как a; тогда площадь треугольника будет равна \displaystyle\frac{\sqrt{3}}{4} a^2. Если обозначим высоту призмы как c, то можно будет выразить ее объем таким образом:
V_\text{призм} = \frac{\sqrt{3}}{2} a^2c.
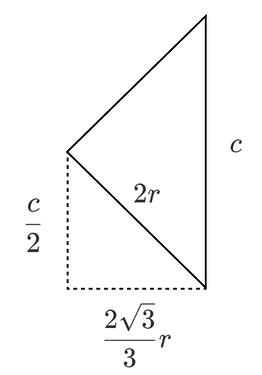
Для ответа на твой вопрос, нам понадобится выразить этот объем через радиус атомов. Легче всего найти a — это расстояние между центрами двух шаров, поэтому a=2r. Немного труднее найти связь между r и c. Возьмем один нижний шар, соединим его центр с ближним зеленым шаром, а потом с центром серого шара, который находится ровно над нижним серым шаром. Тогда у нас получится треугольник. Я прикрепил изображение этого треугольника сбоку.
Это равнобедренный треугольник. Его равные стороны равны 2r, потому что это расстояния между центрами шаров, а основание равно c. Если вернуться к виду сверху, можно увидеть, что проеция стороны 2r — это расстояние от центра серого шара до проекции центра зеленого шара. А проекция центра зеленого шара — это центр равностороннего треугольника, который получился в самом начале, когда мы разделили ромб. Эта точка является пересечением мединаны, высоты и биссектрисы треугольника, поэтому все расстояние равно \displaystyle\frac{2\sqrt{3}}{3}r. По теореме пифгора можно найти связь между c и r и переписать выражение для объема призмы.
\begin{gathered}
c = 4r \sqrt{\frac{2}{3}} \\
V_\text{призм} = 8 \sqrt{2} r^3
\end{gathered}
Теперь найдем количество шаров в одной призме. Сначала может показаться, что все трудно посчитать, но видно, что от серых шаров отсекаются два куска по \displaystyle\frac{1}{6} шара и два куска по \displaystyle\frac{1}{3} шара. И с зеленым то же самое — от зеленого отрезаются два странных куска, но зато те же два странных куска остаются и с другой стороны; значит, в одной такой призме ровно один зеленый шар. Итого у нас 1 серый[1] и 1 зеленый шар — 2 шара.
Объем шара равен \displaystyle\frac{4}{3} \pi r^3. Теперь мы можем посчитать \alpha, то есть соотношение занятого объема на весь.
\alpha = \frac{ 2 \cdot \frac{4}{3} \pi r^3 }{ 8 \sqrt{2} r^3 } = \frac{\pi}{3\sqrt{2}} \approx 0.74
Это значение в точности совпадает с таким же показателем для fcc (face-centered cubic) решетки.
[1] Вообще, мы соединяли центры шаров, поэтому там отрезаются не \displaystyle\frac{1}{6} и \displaystyle\frac{1}{3} шара, а в два раза меньше. Это компенсируется тем, что у нас два уровня серых шаров. Здесь поделим на два, а потом умножим, но в конце получим то же самое — 1 серый шар на каждую призму.
8 лайков
огромное вам спасибооо!!! всё понятно. теперь я не буду затрудняться в таких задачах
2 лайка
