Движущийся прямым курсом со скоростью u = 25 км/ч
катер буксирует бакен (1) и спортсмена на водных лыжах (2). Используется один практически нерастяжимый буксировочный трос,
переброшенный через небольшой блок, закреплённый на корме катера. В некоторый момент времени бакен движется одним курсом
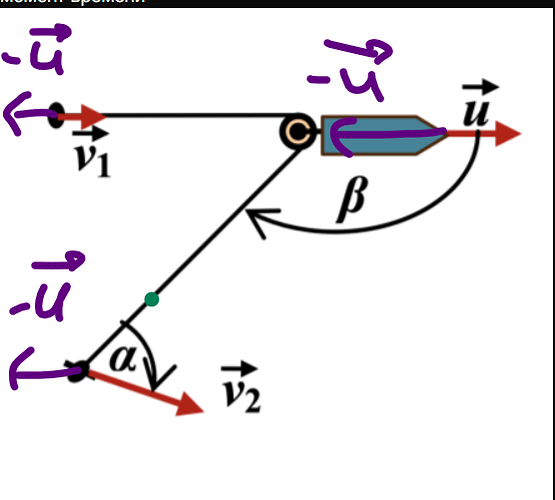
с катером со скоростью v1, равной половине скорости катера, а вектор скорости спортсмена составляет угол α = 60◦
с направлением
троса, причём трос составляет угол β = 135◦
с направлением движения катера (см. рисунок). Найдите величину скорости спортсмена в этот момент времени

Ну здесь, как и почти во всех задачах с блоками используется то, что верёвка имеет конечную длину.
Лирическое отступление. Рассмотрим систему в которой груз прикреплён к нити, которая может удлиняться и вращается вокруг центра.
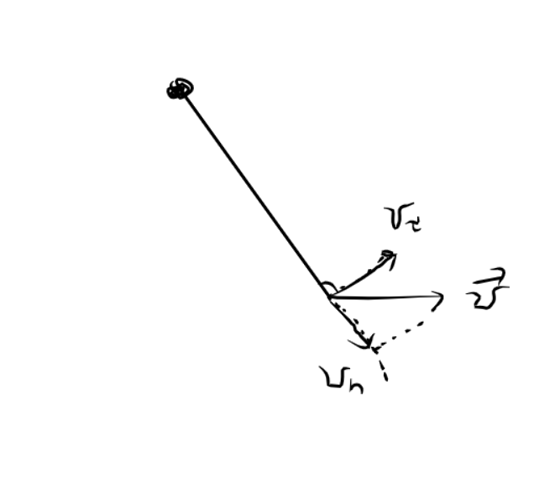
Движение груза можно разбить на две части:
-
Нормальное движение, то есть движение по нормали к касательной, то есть вдоль нити (проекция скорости на верёвку). Оно влияет на длину нити, но не влияет на угол
-
Тангенциальное движение (проекция скорости на касательную к окружности с радиусом, равным длине верёвки). Оно влияет на угол, который пройден верёвкой, но не влияет на длину верёвки.
По Пифагору: v_n^2 + v_\tau^2 = v^2
Вернёмся к задаче. Длина верёвки не изменяется, значит проекции скоростей на верёвку должны быть одинаковыми.
Чего-то не хватает, вам так не кажется? Именно! Не хватает, того, что нужно учитывать скорость катера. Нужно учитывать, что катер движется, а разбивается всё красиво и аккуратно, если центр не движется. Поэтому нам нужно перейти из системы отсчёта Земли, в систему отсчёта катера, векторно отняв у каждого тела скорость катера
Теперь остаётся найти новые скорости и их проекции на концы верёвки