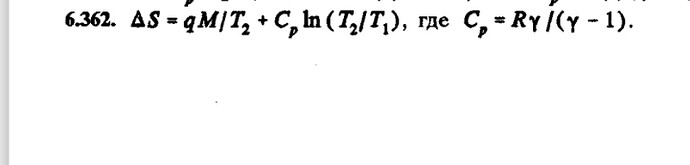Один моль воды, находившийся в равновесии с пренебрежимо малым количеством своего насыщенного пара при
температуре T1, перевели целиком в насыщенный пар при температуре T2. Полагая, что удельная теплота парообразования
практически не зависит от T и равна q, найти приращение энтропии системы. Пар считать идеальным газом, удельным объемом жидкости пренебречь по сравнению с удельным объемом
пара. Помогите решить пожалуйста. Пробовал решить, но в ответе не сходится с Mq/T2
Количество теплоты, необходимое для нагрева воды:
dQ = C_p dT
Приращение энтропии:
\Delta S_{нагрев} = \int \limits_{T_1}^{T_2 }{\dfrac{C_p dT}{T}} = C_p \ln{\dfrac{T_2}{T_1}}
где C_p = \dfrac{R{\gamma}}{\gamma - 1} - молярная теплоёмкость водяного пара при постоянном давлении.
Так как теплота парообразования на единицу массы равна q, то на 1 моль воды потребуется теплота qM, а изменение энтропии будет:
\Delta S_{испарение} = \dfrac{qM}{T_2}
Суммируя, получаем полгое приращение энтропии:
\Delta S = C_p \ln{\dfrac{T_2}{T_1}} + \dfrac{qM}{T_2};
Получили правильный ответ:
1 лайк
Я увидела что вы у меня спросили.
Мы использовали именно C_p,потому что нагревание воды происходит при постоянном давлении(атмсоферном), а при таких условиях теплоемкость системы определяется именно как C_p.
В прошлой задачи написанно что, водянной пар сжимают(расширяют), так, что он все ремя остается насыщенным, значит можете использовать этот вывод с теплоемкостью
2 лайка