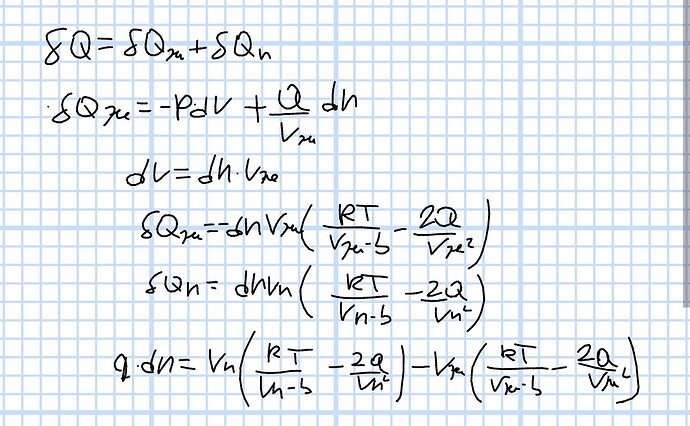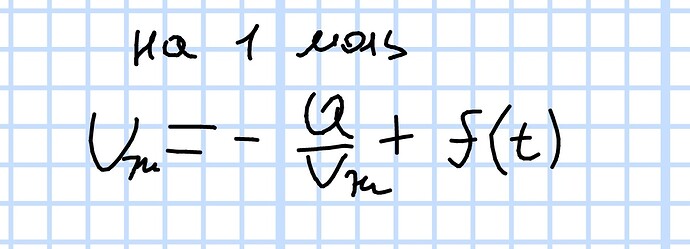Найти выражение для молярной теплоты испарения жидкости при постоянной температуре T под давлением её насыщенного пара в предположении, что и жидкость и пар подчиняются уравнению состояния Ван-дер-Ваальса.
Я не совсем понимаю, что здесь нужно делать, пробовал из уравнения Ван-дер-Ваальса выразить неизвестные для уравнения Клапейрона-Клаузиса, но тщетно, к тому же начала напрягать производная по температуре в этом уравнении, так как температура не меняется, как брать тогда?
У меня есть такое решение:
Рассказываю по порядку:
Тепло системы распишем как сумму тепла пара и жидкости.
Распишем тепло каждой фазы по отдельности.
Получается что какая та часть жидкости испарилась, тоесть объем уменьшаться общий, значит работа минус, объем уменьшился на (моли жидкости*молярный объем).
Давление выражаем из уравнения Вандер ваальса.
Используя формулу внутренней энергии газа Вандер ваальса, можно записать изменение внутренней энергии жидкой фазы, оно положительно так как жидкость “исчезла” а её потенциальная энергия была отрицательная значит в итоге плюс.
(Тут температура постоянная поэтому часть формулы внутренней энергии учитывающая тепловое движение частиц можно не записывать, так как оно зависит только от температуры и она не меняется. )
Точно так же только наоборот со знаками выражаем тепло пара, учитывая что моли для обеих фаз одинаковые, потом суммируем и делим обе части на dn
Насчёт производной в уравнении Клаузиуса клайперона, она даёт градиент графика PT двухфазного состояния. Оно будет полезно если мы знаем общую функцию давления от температуры в двухфазном состоянии, но она не дана.
Температура постоянная именно при фазовом переходе, если представить это на графике РТ то наша задача всё время происходит в одной точке графика. Поэтому не зная градиента в этой точке, мы не сможем использовать уравнение Клаузиуса клайперона.