Apply electromagnetic induction (\xi is e.m.f.)
\xi=\oint_l \vec E\cdot d\vec l = -\frac{d}{dt}\int_S \vec B \cdot d\vec S
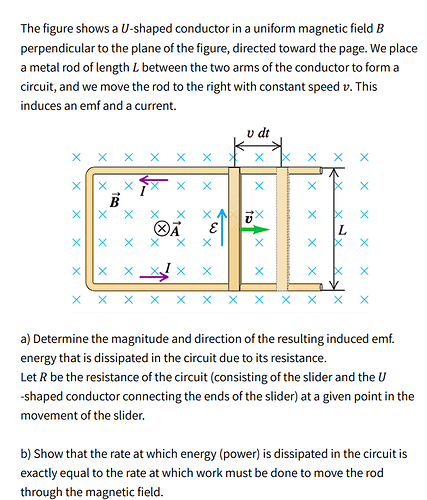
to inner rectangle of conductor. As rectangle expanses, the flux \displaystyle\int_S \vec B\cdot d\vec S increases. Field \vec B is uniform, and S(t) = L\cdot vt, thus \xi = -BLv, where the “minus” sign defines the direction of induced current I=\xi/R(t), and in this problem the current is directed counter-clockwise. R(t) is the resistance of system as a function of time (if \rho=\text{const}, then R(t)=2\rho (L+vt)).
Next, the magnetic field exerts a Lorentz force (F = BIL) on induced current (directed left). I’ve explained this problem using dynamics, but there should be an energy approach, which remains on you.
5 лайков
thanks!