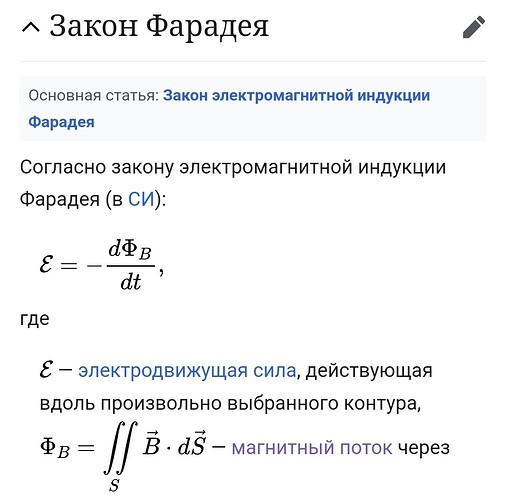
Как можно вывести формулу закона Фарадея, имея школьные знания по физике и возможно диференциалы.
1 лайк
Можно попробовать нарисовать контур с перемычкой,которая будет двигаться,например,вправо ,тогда магнитный поток будет уменьшаться , потому будет изменяться площадь контура.Значит в контуре будет возникать индукционный ток,который вы можете направить с помощью правила Ленца .Ток по определению -это направленное движение электрических зарядов.Пусть носители зарядов положительны.Вы перемещаете проводник и соотвественно заряды тоже перемещаются .На движающий заряженную частицы в магнитном поле действует сила Лоренца ,которую вы можете разложить на компоненты ,т.к носители зарядов участвуют в двух движениях (вместе с проводником и вдоль него),поэтому скорость носителей зарядов будет направлена под углом.Дальше вы можете расписать работу этих сил по определению и прийти к формуле
E=BVL,V=dx/dt ,дальше преобразование и приходите к формуле закона электромагнитной индукции .
Вообще это можно вывести через рассмотрение магнитного потока напрямую, здесь еще надо знать определение эдс. Обозначим вектор магнитной силы действующую на заряд как \vec F=q(\vec v\times\vec B), тогда эдс равен работе этой силы на единицу заряда
\mathcal{E}=\frac{1}{q}\int \vec F\cdot\vec {dl}=\int(\vec v\times\vec B)\cdot\vec{dl}
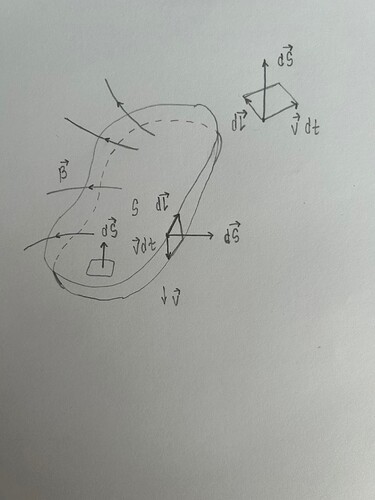
Рассмотрим какой-то контур S, каждый элемент dS которого перемещается со скоростью v в новое положение в интервале времени [t, t+dt]. Магнитный поток через такой контур в момент времени t:
\Phi(t)=\int_S\vec B\cdot\vec {dS}
А в момент времени t+dt поток становится:
\Phi(t+dt)=\int_{S+dS}\vec B\cdot\vec {dS}=\Phi (t)+\int_{dS}\vec B\cdot\vec dS
Далее воспользуемся определением дифференциала
\Phi(t+dt)-\Phi(t)=d\Phi=\int_{dS}\vec B\cdot\vec {dS}
Теперь вектор \vec{dS} нужно выразить через вектор скорости \vec v и вектор \vec {dl}
Как показано на рисунке пусть вектор скорости \vec v будет направлен вниз, то что “сверху” это положение контура в момент времени t, а то что “снизу” и частично заштриховано
это положение контура в момент времени t+dt. Вектор \vec {dS} элемента поверхности контура всегда направлен по нормали к его поверхности: \vec{dS}=\hat n( dS), тогда как вектор элемента длины \vec dl направлен по касательной к его поверхности. По "правилу правой руки " или другим правилом векторного произведения можно показать что \vec {dS}=(\vec vdt)\times\vec {dl}. Подставляя это в выражение для магнитного потока
d\Phi=\int_{dS}\vec B\cdot\vec {dS}=\int_{dS}\vec B\cdot (\vec vdt\times\vec {dl})\rightarrow \frac{d\Phi}{dt}=\int_{dS}\vec B\cdot(\vec v\times\vec {dl})
По правилу векторного произведения \vec a\cdot(\vec b\times\vec c)=\vec b\cdot(\vec c\times\vec a)=\vec c\cdot(\vec a\times\vec b). Используя это верхнее выражение можно преобразовать
\frac{d\Phi}{dt}=\int_{dS}\vec B\cdot(\vec v\times\vec {dl})=\int_{dS}\vec {dl}\cdot(\vec B\times\vec v)=-\int_{dS}(\vec v\times\vec B)\cdot\vec {dl}
Сравнивая это с выражением для эдс (сверху), приходим к тому, что
\mathcal{E}=\int_{dS}(\vec v\times \vec B)\cdot \vec{dl}\rightarrow\mathcal{E}=-\frac{d\Phi}{dt}
Закон Фарадея для электромагнитной индукции также можно вывести рассмотрев движение прямоугольного контура в неоднородном магнитном поле. Это можешь взять как домашнее задание и показать учителю на уроке
5 лайков