1 лайк
Anyone?
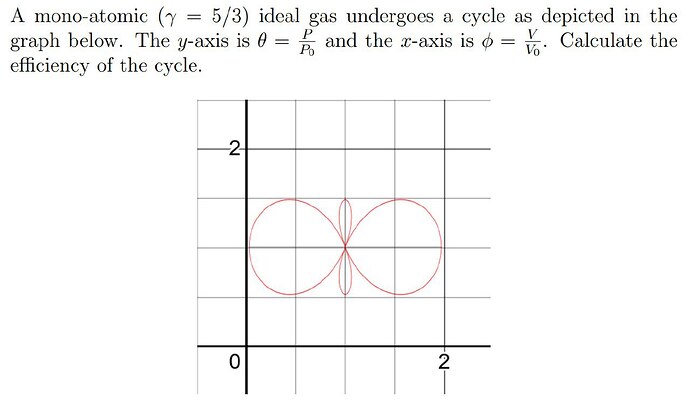
what’s the direction of a cycle?
1 лайк
direction is clockwise…
The solution starts very similarly to what Ersultan provided in Entropy-Temperature graph problem, try to think of it this way.
1 лайк
I am not able to figure it out… 
what answer are you getting? the answer given is: 0.1493
The work of a gas is obtained via integrating the 1st thermodynamics law
\oint \delta Q = \oint dU + \oint PdV = \oint PdV = A.
The efficiency is a fraction between A and positive heat Q_+, so we should calculate the latter:
\int_{\delta Q>0} \delta Q = U_2 - U_1 + \int_{\delta Q > 0}PdV.
So we have to find points where \delta Q changes its sign, and these are simply the points where infinitesimally small adiabatic processes are proceeded, or, in other words, the points where the slope is
\frac{dP}{dV} = -\gamma\frac{P}{V}\quad\Rightarrow\quad\frac{d\theta}{d\phi}=-\gamma\frac{\theta}{\phi}.
I’m not so sure how to find numerical values of these points. This cycle looks like mutually perpendicular lemniscates of Bernoully, so maybe we can somehow go into polar coordinates?
3 лайка
Pretty cringe problem tbh
1 лайк
This was from modified from Rudolf Ortvay 2015 problem
Yeah polar coordinates is the way to go i believe, considering we can make an equation of curve (on wolfram)
1 лайк