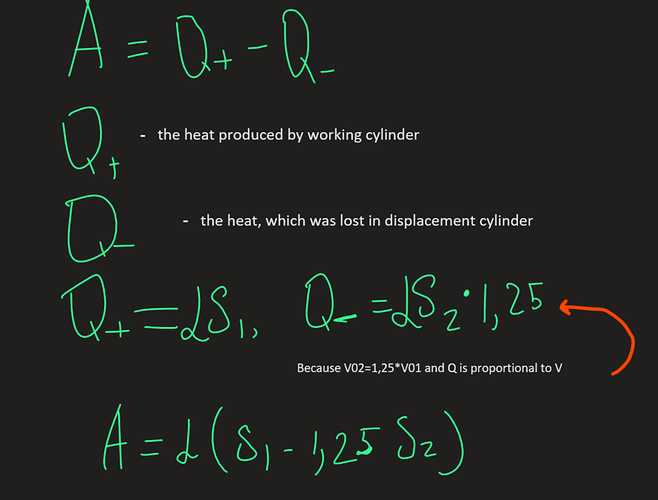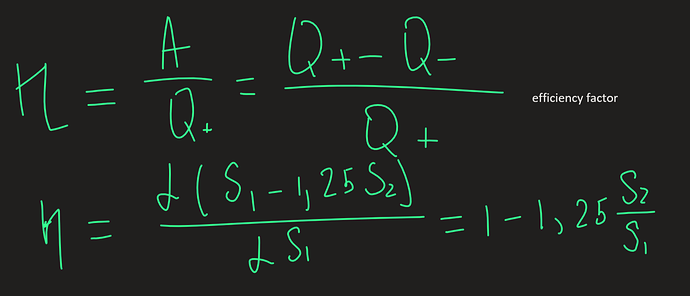Link to the Russian translation: https://mathus.ru/olymp/MosPhys2019tur2-10.pdf
Firstly, let’s take a closer look at pV diagrams:
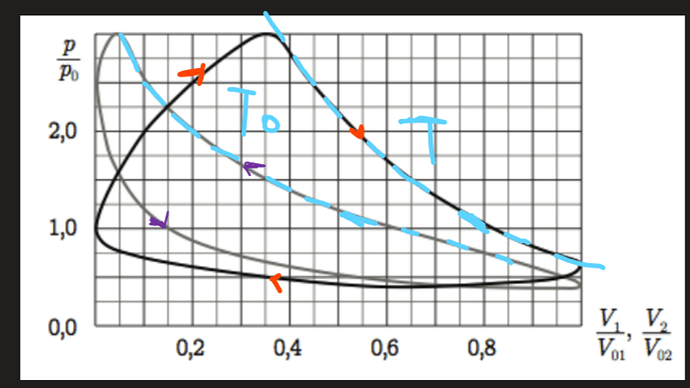
Working cylinder’s cycle directed clockwise, displacement cylinder’s cycle directed counterclockwise. For constant temperatures in cylinders, we should have isotherms in their cycles:
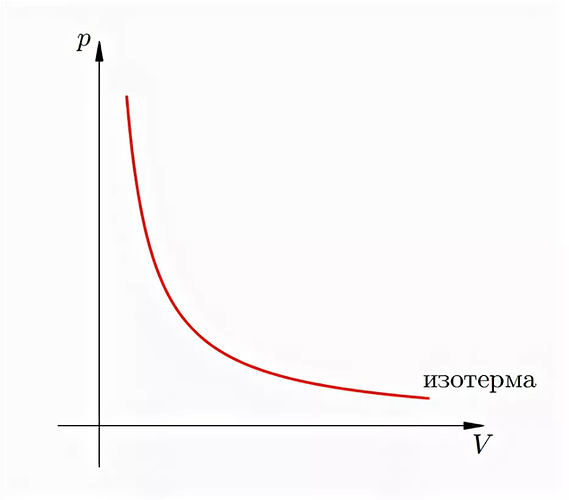
It’s obvious that the line I highlighted with blue in the working cylinder’s cycle is an isotherm because isotherms should look like that (and other parts of the working cylinder’s cycle don’t look like that):
For the displacement cylinder, we take the higher part of the gray line as an isotherm, because according to the problem the primary function of the displacement cylinder is to compress (gas). In that part, you can see that volume is decreasing.
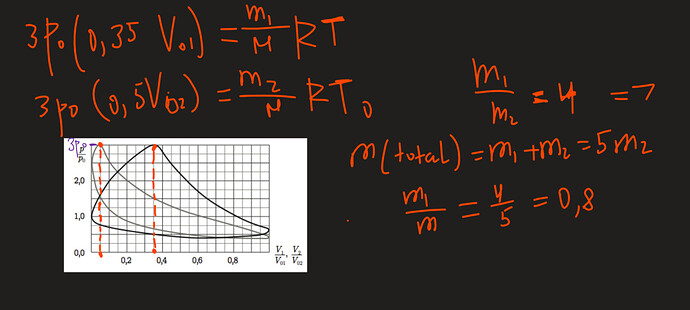
Using the equation of state for two points in isotherms we have an answer(with little error):
The total mass of air consists of air that is in a working cylinder and air that is in a displacement cylinder. That’s why we write again use equations of state (for points where pressure 3p0) to find masses :
( again the answer has a little error, which is normal)
The definition of work:
Therefore the work is just the area under the graph in pV diagram. We can assume that heat is proportional to the area
Working cylinder produces heat, displacement cylinder compresses the gas and lowers the temperature:
(where a is just proportionality coefficient)
Using the definition of efficiency factor we get the formula to calculate it:
You can calculate (roughly) the area under the two lines and get an answer by yourself
here the whole thing is an isotherm (because the \nu is not conserved for one of the cylinders), and that highlighted part just appears to be a normal isotherm (an isotherm where \nu=\text{const}), but still it is not. If you calculate T/T_0 by taking other dots of the graph (say, 0.4V_1/V_{01}, not 0.6), you won’t get the same numerical result. The solution for other parts of the question are ok, though
Thanks a lot! It was really helpful.
Sorry, I am unable to understand what you are saying. Could you please elaborate?
Извините, я не могу понять, что вы говорите. Не могли бы вы уточнить?
According to the task, the temperature in both cylinders always remains constant.
Within the framework of this model it is considered that its temperature is maintained constant
A radiator is fixed on displacement cylinder… the temperature in the cylinder is assumed to be equal to the room temperature
And the isotherms have such strange shape because \nu of air in cilynders is not constant. Otherwise the graphs of the isotherms would have hyperbolic shape