Problem based on Surface Tension | Soap film between two rings

[Arthur]

Can anyone please provide a solution to the 3 parts of this problem? I was unable to solve this on my own. It will be very helpful. Thanks!
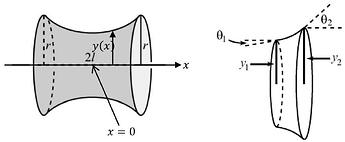
Problem: Consider the soap membrane suspended between two ideal rings with radius
r, as shown in the left figure below, the planes where the two rings are located
are both perpendicular to the connecting line between the two centers. The
distance between the two rings is 2ℓ. In the case of constant temperature, the
surface tension of the film is constant. We set the x coordinate axis parallel
to the line connecting the two circle centers, and the origin is at the midpoint
of the two circle centers. Assuming that the section radius at the abscissa x
is y(x), and the angle between the membrane and the x axis is \theta, as shown
in the right figure below. This question does not take gravity into account.

1. Please prove that y(x) · cos \theta = constant.
2. If there is a constant b such that:
   r = \frac{1}{b} * cosh bl
   Find the equation y(x) of the shape of the soap film.(expressed in b
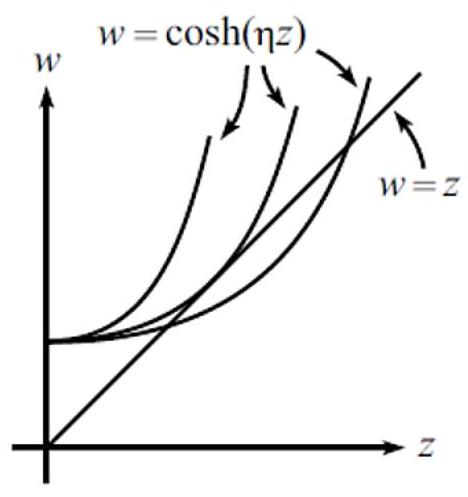
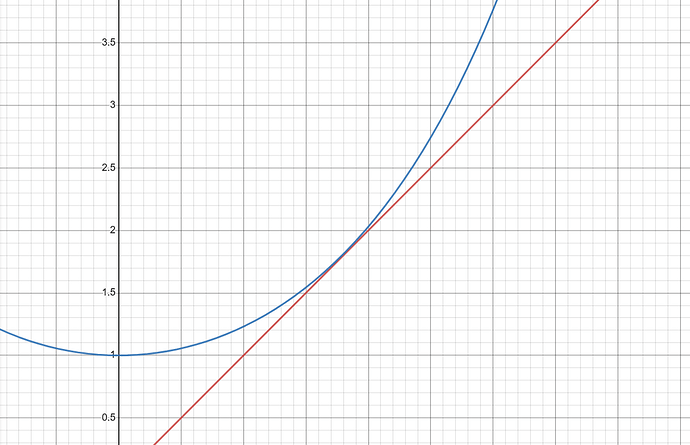
   and x)
3. To make these membranes exist stably, a constant b must be found to satisfy r=\frac{1}{b} \cosh b \ell, but once \ell / r is greater than a certain critical value, b does not exist. If the function graph of w=\cosh \eta z and w=z is known as follows, the three curves in the figure correspond to different values of \eta respectively. When \eta<\eta_{0}, there are two intersections between w=\cosh \eta z and w=z; when \eta>\eta_{0}, there is no intersection between w=\cosh \eta z and w=z; and when \eta=\eta_{0}, there is exactly one intersection. If \eta_{0} \approx 0.663 is obtained through calculation, try to find the maximum value of \ell / r that enables the membrane to exist stably.

Hint: \int \frac{1}{\sqrt{x^{2}-1}} d x=\ln \left(\sqrt{x^{2}-1}+x\right)+ Constant, \cosh x=\frac{e^{x}+e^{-x}}{2}.

Answers given: (1) Prove yourself. \quad (2) y(x)=\frac{1}{b} \cosh b x \quad (3) The maximum value of \ell / r is \eta_{ 0} \approx 0.663

Diagrams:

[Damir (Yekibayev Damir)]

This problem is more mathematical than physical. Consider a ring of radius y (the radius is y because the horizontal axis divides the surface of revolution into two symmetrical parts) and thickness ds, its area dA=2\pi y ds

Taking it into account we can find the area of the whole surface of revolution (we also need to take into account the fact that unit lenght of the curve is ds=\sqrt{dx^2+dy^2})

A=\int 2\pi yds=\int 2\pi y\sqrt{1+\left(\frac{dx}{dy}\right)^2}dy=\int 2\pi y \sqrt{1+x'^2}dy

Now we should use the analogy with the Lagrangian method to find minimize the surface area. In mechanics we use the Lagrangian technique to minimize the action: S=\int \mathcal Ldt=\int (K-U)dt\rightarrow \min and we also have the general Euler-Lagrange equations: \left(\frac{\partial \mathcal L}{\partial q_i }\right)=\frac{d}{dt}\left(\frac{\partial \mathcal L}{\partial \dot q_i}\right). We can use all of that in this situation too, because here we want to minimize the integral:

A=\int 2\pi y\sqrt{1+x'^2}dy\rightarrow \min

To evaluate the y(x) we should make appropriate substitutions, thus the time in integral S=\int \mathcal Ldt becomes t\rightarrow y and the Lagrangian in this case is \mathcal L\propto y\sqrt{1+x'^2}. Th Euler-Lagrange equation for this problem is \left(\frac{\partial \mathcal L}{\partial x}\right)=\frac{d}{dy}\left(\frac{\partial \mathcal L}{\partial x'}\right). If we take the first partial derivative then we notice that:

\mathcal L\propto y\sqrt{1+x'^2}\Rightarrow \frac{\partial \mathcal L}{\partial x}\propto\frac{\partial }{\partial x}\left(y\sqrt{1+x'^2}\right)=0

And we use the Euler-Lagrange equation:

\left(\frac{\partial \mathcal L}{\partial x}\right)=\frac{d}{dy}\left(\frac{\partial \mathcal L}{\partial x'}\right)\Rightarrow \frac{d}{dy}\left(\frac{yx'}{\sqrt{1+x'^2}}\right)=0\Rightarrow \left(\frac{yx'}{\sqrt{1+x'^2}}\right)=const=C

It’s really convenient to write the last equation in another form and then we can evaluate the integral:

\frac{yx'}{\sqrt{1+x'^2}}=\frac{y}{\sqrt{1+y'^2}}=\frac{y}{\sqrt{1+\left(\frac{dy}{dx}\right)^2}}=C\rightarrow \int \frac{dy}{\sqrt{(Ay)^2-1}}=\int dx

Here I made the comfortable substitution A=\frac{1}{C}. Here we use the table integral for hyperbolic function: \int \frac{d\xi}{\sqrt{\xi^2-1}}=\cosh^{-1}+C and get the function y(x):

y(x)=\frac{1}{\sqrt A}\cosh\sqrt A(x+c)=\frac{1}{a}\cosh a(x+c)

Here \sqrt A=a. Now we know the shape of the curve, to obtain the constants we use conditions y(l)=y(-l)=r and r=\frac{1}{b}\cosh bl and obtain the function y(x)=\frac{1}{b}\cosh bx. Now let’s look at the equation r=\frac{1}{b}\cosh bl, if we denote \eta=\frac{l}{r} then l=\eta r. If we now put the l into equation br=\cosh \eta br. We can denote br as z, so

\cosh(\eta z)=z

This is a transcendental equation and it is easy to solve it with drawing the graphs of the each functions on the left and right sides of the equation. (look at it as if we have two functions \xi_1(z)=\cosh (\eta z) and \xi_2(z)=z and we need to find the z so that \xi_1(z)=\xi_2(z))

You can use the graphical calculator and by changing the value of \eta find the critical value of \eta when the curve \cosh (\eta z) touches the line z. The critical value is approximately

\eta_{crit.}\approx0.65

Which is pretty close to the answer. (we just needed to estimate \eta_{crit.}).
It’s easy to prove that y(x)\cos\theta =const, once we know that y(x)=\frac{1}{b}\cosh (bx) and by definition \cos \theta =\frac{1}{\sqrt{1+\tan\theta^2}}=\frac{1}{\sqrt{1+\left(\frac{dy}{dx}\right)^2}}. Using the definition of hyperbolic functions we get

\sinh (bx)=\frac{e^{bx}-e^{-bx}}{2}\quad \cosh (bx)=\frac{e^{bx}+e^{-bx}}{2}\rightarrow \frac{dy(x)}{dx}=\sinh (bx)

From the first two equations above we can prove that \cosh^2(bx)-\sinh^2(bx)=1. Hence the \cosh (bx)=\sqrt{1+\sinh^2(bx)}. Finally

y(x)\cos\theta=\frac{1}{b}\cosh(bx)\left(\frac{1}{\sqrt{1+\sinh^2(bx)}}\right)=\frac{1}{b}=const

[Arthur]

Amazing!
Thanks a lot.