Каркас сила натяжения

[Azor-Ahai (Azor)]

• условие:
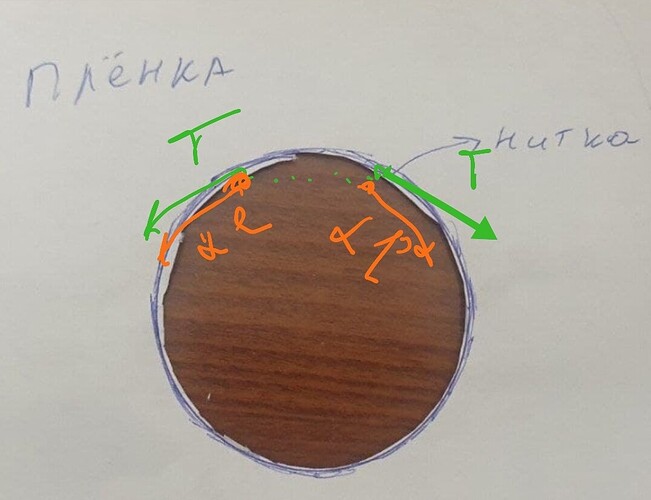
  На плоский каркас натянута мыльная пленка. На ней находится петля из нити. После того, как пленку прокололи внутри петли, последняя приняла форму окружности радиуса R = 7,5 мм. Найти силу натяжения нити, если поверхностное натяжение мыльной воды а = 40 мН/м.
• не понимаю во первых как это выглядеть будет
• решил следующе:
  (1) T = 2 \pi r умножить на \sigma \text{(пов натяж)} делить на \pi r^2

[Azor-Ahai (Azor)]

офигеть какой latex трудный

[ernur045 (Yernur Kairollayev)]

@Azor-Ahai

решил следующе:
(1) T = 2 \pi r умножить на \sigma \text{(пов натяж)} делить на \pi r^2

Нет, не так

Подсказка

Рассмотри малый участок нити и силы действующие на него

[Azor-Ahai (Azor)]

Я почему то слепо считал каркас прямоугольной формы

[ernur045 (Yernur Kairollayev)]

Так нам форма каркаса не важна же. Только у нитки решает

[Azor-Ahai (Azor)]

А как так получается что теншионы тянут результирующей силой в сторону центра круга

Также и с поверхностным натяжением которая также тянет во внутрь

[ernur045 (Yernur Kairollayev)]

@Azor-Ahai

А как так получается что теншионы тянут результирующей силой в сторону центра круга

Нарисуй малый участок нити, и нарисуй силы, которые действуют на него.

@Azor-Ahai

Также и с поверхностным натяжением которая также тянет во внутрь

Оно тянет наружу, и опять же нарисуй малый участок нити и силы, действующие на него

[Azor-Ahai (Azor)]

Нарисовал и так и получилось как написал ввыше

И еще не понял следующее выражение:
+пленку прокололи внутри петли

Значит ли это что это уже не мыльная пленка
И что там 1alpha вместо двух

[ernur045 (Yernur Kairollayev)]

@Azor-Ahai

И еще не понял следующее выражение:
+пленку прокололи внутри петли
Значит ли это что это уже не мыльная пленка

Ну нитка “разделяет” мыльную плёнку на 2 части. Внутреннюю прокалывают, а внешняя остаётся целой благодаря нитке. Это всё ещё плёнка.

Ну и вот немного подкорректированный рисунок. Из симметрии выходит, что силы натяжения нити налево и направо равны. А сила поверхностного натяжения плёнки тянет наверх вдоль радиуса. Так можно говорить потому что участок нити маленький, следовательно изгиб тоже очень маленький, следовательно его можно считать прямолинейным (когда считаешь результирующую силу натяжения нити, такую аппроксимацию^[1] делать не надо, нужно делать другую)

---

1. 
   

   
   
   ↩︎

[Azor-Ahai (Azor)]

Ответ подходит лишь тогда когда беру пов натяжение равным 2a
Но по условию там ведь должен быть лишь 1a

[ernur045 (Yernur Kairollayev)]

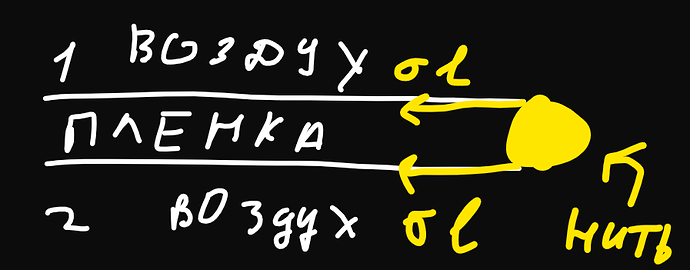
Сколько поверхностей у мыльной плёнки?

[Azor-Ahai (Azor)]

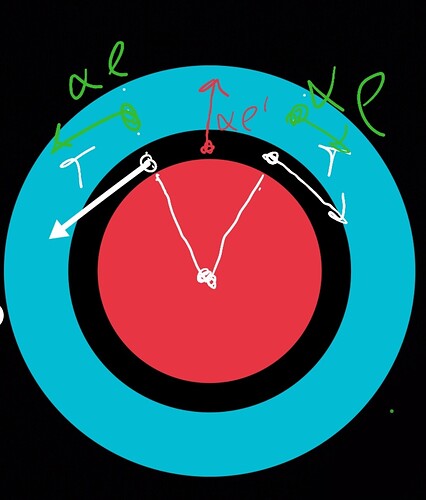
Вот так понимаю задачу

Красный - внутренний слой пузыря
Черный - сила натяжения веревки
Голубой - внешний слой

[Kirill_Chumikov]

@Azor-Ahai

Ответ подходит лишь тогда когда беру пов натяжение равным 2a

Так и правильно.Ты учитываешь,что у тебя две поверхности пленки,записав 2а.

[Azor-Ahai (Azor)]

Понимаю, но просто веревка стоит между этими слоями, поэтому она разве не меняет направление некоторых сил?

[ernur045 (Yernur Kairollayev)]

@Azor-Ahai

Вот так понимаю задачу

Красный - внутренний слой пузыря
Черный - сила натяжения веревки
Голубой - внешний слой

Да, и внутренний слой лопается → он не влияет на систему

@Azor-Ahai

Понимаю, но просто веревка стоит между этими слоями, поэтому она разве не меняет направление некоторых сил?

Хорошо, как ты представляешь этот процесс?

А ещё, ты не ответил на вопрос:

@ernur045

Сколько поверхностей у мыльной плёнки?

Но ответил @Kirill_Chumikov, так что в принципе отвечать уже не надо

[Azor-Ahai (Azor)]

@Azor-Ahai

2 слоя но по условию один из них лопается
Значит 1a

Две части, одна из них лопается. У плёнки есть две поверхности, где она контактирует с воздухом

[Azor-Ahai (Azor)]

@ernur045

Хорошо, как ты представляешь этот процесс?

Именно этот момент не особо понимаю в решении

Ведь даже если аппроксимацией брать то она должна или сократиться по горизонтали(так как взяли как прямую) или направиться радиально к оси