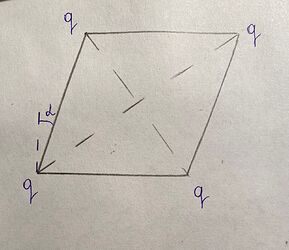
I was trying to solve this problem but I could not formulate any ideas. How would you rate this task in terms of difficulty? Please provide some insight in all 3 parts as well.
-
For the first part you can consider changes in energy for the soap film and electric potential energy for charges. Under perturbations square film will become a rhombus with angles close to 90^{\circ}.
\displaystyle \delta E_\sigma =\sigma l^2\cos(\alpha) - \sigma l^2 \thickapprox - \sigma l^2\frac{\alpha^2}{2}
\displaystyle \delta E_e = \frac{kq^2}{\sqrt{2}l} \left( \frac{1}{1-\sin(\frac{\alpha}{2})} + \frac{1}{1+\sin(\frac{\alpha}{2})} -2\right) \thickapprox \frac{kq^2}{2 \sqrt{2}l}\alpha^2
For stable perturbations total change in potential energy must be positive, so condition is
\displaystyle \frac{kq^2}{\sqrt{2}l} > \sigma l^2 -
For the second part surface area of the film must be minimum, meaning that
\displaystyle A= \int \sqrt{ 1 +\left( \frac{\partial z}{\partial y}\right) ^2 + \left( \frac{\partial z}{\partial x}\right) ^2} dx dy = min. For this functional you can write the Euler-Lagrange equation:
(Minimal surface - Wikipedia)
Using the fact that soap film is slightly off the z=0 plane (meaning that z_x, z_y are small), you will get the Laplace equation.
Thank you so much, I’ll read about minimal surface! Also, how would you rate the difficulty of this problem?
Any hints or explanations for the 3rd part?
I think first part is not that hard, and it could be an olympiad problem. Second and third part, however, are difficult and can be considered more as university level physics problems.
Unfortunately, I have no idea how to solve it. Probably you can use the method from the first part and calculate the potential energy of the surface to derive the equations of motion. However, for this method you will need to find analytically z(x, y) by solving the Laplace equation with the given boundary conditions, and I don’t know how to do that.
Oh I see. This problem was a part of a mock test given to me for olympiad practice. I think this problem is probably overkill then. If you are not getting idea of part 3, then it would be best for me to leave this problem part altogether. I dont know how people create such problems? I put over 4 days in this question and no progress until now.
Btw, I tried reading about minimal surface etc. But it went over my head. Could you please elaborate the part 2 with more steps? ![]()
Sorry, but the answer of the first part is kq^2 >\frac{4\sqrt{2}}{3} \sigma l^3
Any progress, sir?
For the second part you can think of function \displaystyle \sqrt{1 + \left(\frac{\partial z}{\partial x} \right)^2 + \left(\frac{\partial z}{\partial y} \right)^2} in surface integral as of Lagrangian \displaystyle \mathcal{L} \left(x, y, z, \frac{\partial z}{\partial y}, \frac{\partial z}{\partial x} \right).
Then you can write the Euler-Lagrange equations:
{\displaystyle {\frac {\partial {\mathcal {L}}}{\partial z}}-\sum _{j=1}^{n}{\frac {\partial }{\partial x_{j}}}\left({\frac {\partial {\mathcal {L}}}{\partial z_{j}}}\right)=0}, where x_j=x, y and \displaystyle z_j = \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}
Since \mathcal {L} does not depend on z you will get \displaystyle {\frac {\partial }{\partial x}}\left({\frac {\partial {\mathcal {L}}}{\partial z_{1}}}\right) +{\frac {\partial }{\partial y}}\left({\frac {\partial {\mathcal {L}}}{\partial z_{2}}}\right) =0
After differentiating you will get the equation for minimal surface. There you can neglect the terms with z_x, z_y since perturbation is small.
Then they must have considered perturbations in 3 dimensions for the 1 part. I assumed that they meant perturbations in 2D because motion and shape of frame in 3D is analyzed in parts 2 and 3. I think that finding conditions for stable perturbations in part 1 makes no sense because it requires you to already know the z(x, y) and finding potential energy of the system, which makes parts 2 and 3 meaningless.
I made some progress in 3 part and found that by using separation of variables for the Laplace equation we can get z = z_0 \cosh(ky) \cos(kx). (x, y are the coordinates along the diagonals of the frame) We can apply boundary conditions for positions of hinges and take two of them to be on the z=0 plane. By calculating the surface integral with approximation that z is small and z_x, z_y << 1 we can obtain potential energy of the film. However, integral will look like this:
\displaystyle \int_0^{\frac{a}{\sqrt{2}}}\int_0^{\frac{a}{\sqrt{2}}-y} \frac{k^2z_0^2}{2} \left(\cos(ky)^2\sinh(kx)^2 + \sin(ky)^2\cosh(kx)^2 \right) dx dy
It is solvable by using right approximations and integral calculator, but I think there must be some easier way to solve this problem.
Thanks!
Don’t even ask me how is it possible to solve this in exam… i dont have the answer😭
that’s a complete overkill dude
100% i think these are the problems to be skipped in exam
language, please.
Oh, I am really sorry, I did not know it was restricted.
it’s a forum in which 90% of users are students of 8-12th grades
Yeah that is true… But how does it correlate to restricting words… Anyways, rules are rules… So, I’ll adhere.