This is the question, I am unable to understand the solution even after translating because Google Translate isn’t that good/clear. Could anyone please explain the solution or just translate it into simple english if possible, so that I may understand it better?
The solution is quite hard even for those who understand Russian. With my own explanation I hope to clarify the proposed solution.
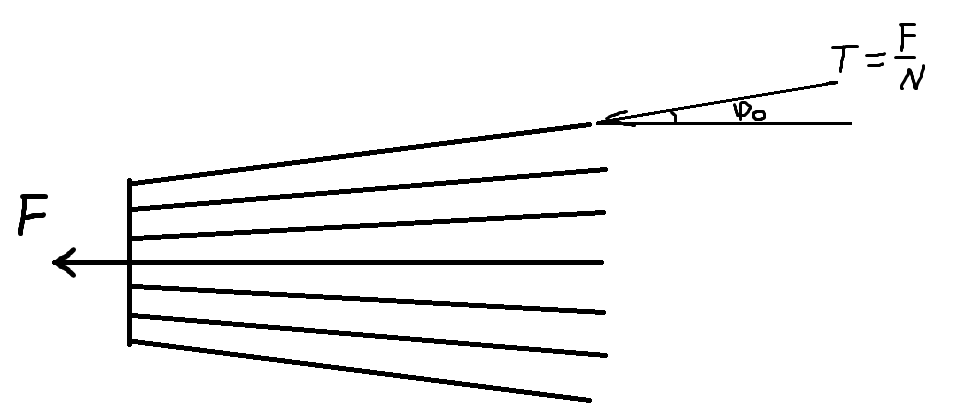
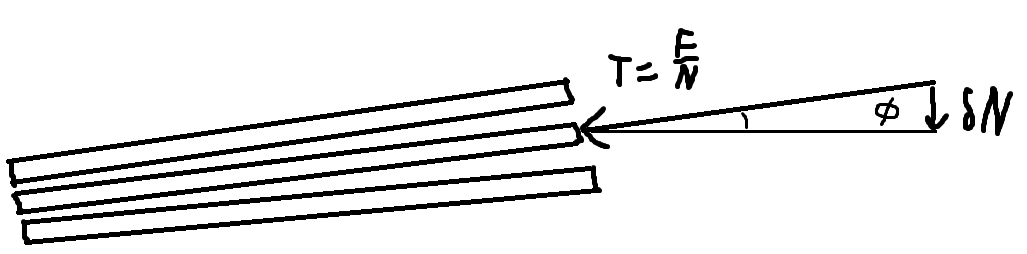
The main idea is concluded in proportionality of friction force to external one. Let’s not introduce the total angle \phi_0 between outer and middle sheets of paper (like in the first picture below), but consider forces that act on arbitrary, n-th sheet (second picture).
The angle between n-th sheet with the middle one equals \phi=\displaystyle n\frac{d}{L/2}. As in the official solution, the tension of n-th sheet equals T=F/N, but due to angular deviation from the middle sheet appears “additional” reaction force \delta R = T\sin\phi\approx T\phi = \displaystyle\frac{2nFd}{NL}. The total reaction force on (n-1)-st sheet is greater than on n-th by 2\delta R because of the n-th sheet from another book, so the total reaction force on n-th sheet equals
R = \sum_{i=n}^{N/2} 2\delta R = \sum_{i=n}^{N/2} \frac{4Fd}{NL}i = \frac{4Fd}{NL}\cdot \frac{(n+N/2)(N/2-n+1)}{2}
Finally, we may calculate the total friction force that acts on the middle sheet (I have doubled the sum because the total force is made up from both sides, and also I’ll be using Wolfram because I’m too lazy):
f= 2\sum_{n=1}^{N/2} \mu R = \frac{4\mu Fd}{NL} \sum_{n=1}^{N/2} (n+N/2)(N/2-n+1) = \frac{8\mu Fd}{NL} \cdot \frac{N(N^2+3N+2)}{24} \approx \frac{\mu d N^2}{3L} F
We need f>F, so N>\displaystyle\sqrt{\frac{3L}{\mu d}}.
P.S. The problem is hard due to its mathematical aspect of finding out how to calculate the “sum of the sum”
\displaystyle\sum_{n=1}^{N/2} \sum_{i=n}^{N/2} i = \frac{N(N^2+3N+2)}{24},
but notice that N>>1, so our calculations may be done a little easier.
Firstly,
\sum_{i=n}^{N/2} i \approx \int_{n}^{N/2} idi =\frac{(N/2)^2 - n^2}{2}.
Then,
\sum_{n=1}^{N/2} \frac{(N/2)^2 - n^2}{2} \approx \int_0^{N/2}\frac{(N/2)^2 - n^2}{2} dn = \frac{(N/2)^3}{2} -\frac{(N/2)^3}{6} = \frac{N^3}{24},
just as we wanted. As far as I remember, the trick of a replacing the sum with an integral was used in Tuymaada olympiad (in Russian Problem 31, but you may find an English version on official website).
6 лайков
Wow! Thanks a lot. You’re a genius!