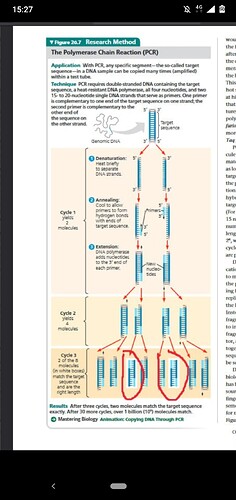
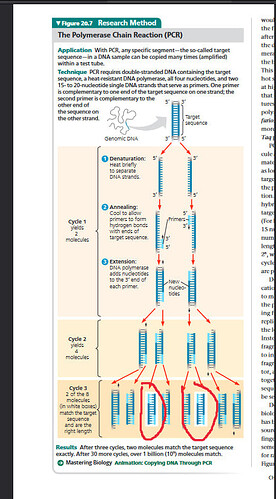
Сколько “чистых” ДНК образуется после 10ти циклов ПЦР? Как рассчитать?
4 лайка
Что вы знаете о выходе в ПЦР? Сколько нужных копий выходит за раз? Что вы знаете о прогрессии 2^n ? Какое у вас есть предположение?
Подсказка : за цикл у нас по 2 копий, то во втором цикле будет 4 (2 новые цепи на 1 цепь синтезированную в прошлый раз), в третьем 8, все идет по прогрессии 2^n . Теперь подставьте под n нужное значение.
Это я знаю, спасибо) Но вот “чистых”, то есть без остатков ДНК имелось в виду…
2 лайка
количество днк без остатков можно посчитать вручную, просто нарисовав, но это будет долго. Поэтому было бы хорошо найти более быстрый способ нахождения кол-во чистых днк
1 лайк
Я это дал в качестве подсказки 
Можно просто подставить под прогрессию 2^n , выходит 2^{10} = 1024 .
Спасибо за подсказку, помогло
3 лайка
Под “чистыми” он имел ввиду те отрезки которые не равны оригинальной молекуле ДНК. То есть при пцр использовали праймеры которые комплементарны к определенному гену (просто например взял), значит не вся ДНК реплицируется. Если так брать то только после 3 циклов получаются первые молекулы ДНК без этих остатков. Вопрос заключается в том что как можно быстро посчитать сколько таких “чистых” ДНК без остатков будет после 10 циклов.
2 лайка
Сори неправильно понял. Могу ошибочно предположить, но можем ли высчитать кол-во чистых ДНК просто умножив \frac{1}{4} \cdot 1024 =256? Можете сказать это правильно @Axolotl ?
n = 2, не проходит
1 лайк
спасибо
1 лайк
есть один вариант проверить, посчитать все вручную или написать код
Думаю нет. Потому что каждый цикл воспроизводит новые “полу-чистые” молекулы, которые потом дают 1 чистую. И если допустим в качестве проверки продолжить 4ый цикл, то у нас получится 8 чистых молекул. По твоей логике если умножать 2^4 * 0.25 будет = 4, а не 8. Так что из за того что у нас каждый раз производятся такие “полу-чистые” молекулы, задача усложняется.
1 лайк
тогда возможно можно сделать некое уравнение/прогрессию для этого? Если да, можете нам помочь?
По идее формулу думаю можно придумать, но уйдет немало времени. Легче просто найти закономерность механический и расписать. Через пару циклов рука уже набьется и можно будет быстро делать. Однако это работает с маленьким количеством циклов, и если нам дадут циклов так 30 то уже надо будет формулу делать. А так ответ = 1004.
Начну с 4 цикла
4) 2 чистых (с 3 цикла) удваиваются и + получистые дают по одному → 2 * 2+4=8
5) 8 чистых с 4 цикла удваиваются и + получистые дают по одному → 8 * 2+6=22
6) 22*2+8=52
7) 52 * 2+10=114
8) 114 * 2+12=240
9) 240 * 2+14=494
10) 494 * 2+16=1004
p.s. Если кто то сделает формулу из того что я расписал, буду рад 
3 лайка
спасибо чувак
2 лайка
the debate is over
3 лайка
получается что это рекурсией решается?
если начать с 4го, когда будут уже 2 “чистые”, то возможно
a_n=a_{n-1} \cdot 2+2 \frac {2}{3} \cdot n
а хотя, это же тоже подбор вручную)
Данная последовательность удовлетворяет данному реккурентному соотношению
a_1 = 0, a_2 = 0, a_3= 2, a_n = 2 * a_{n - 1} + 2\cdot(n - 2), \forall n \geq 4
Методом пристального взгляда)) несложно заметить что
a_n = 2^n - 2\cdot n, \forall n \geq 1
3 лайка
Да, тоже вывел некую формулу
4 * (2^(n-1) - n + 1) + 2n -4
Должно подойти под любые циклы
1 лайк