Не могу решить задачу, как-будто данные должны быть немного иными, в общем 6 неизвестных и 4 уравнения в котором плюс различаются концентрации.
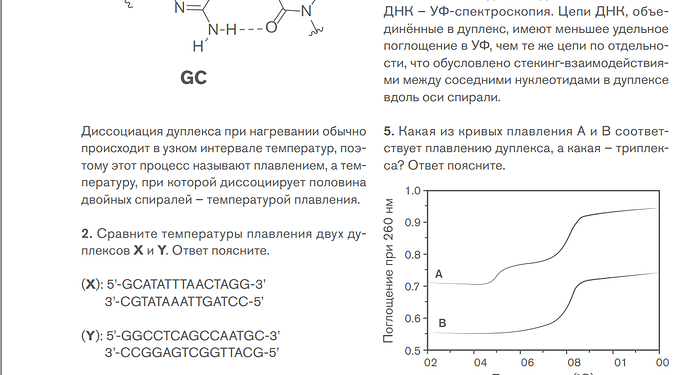
У меня есть идея насчет этой задачи. Как я понял, происходит процесс диссоциации дуплекса, что и называется плавлением (сначала я думал про обычное плавление):
\ce{AB <=> A + B}
K = \frac{ [\ce{A}] [\ce{B}] }{ [\ce{AB}] }
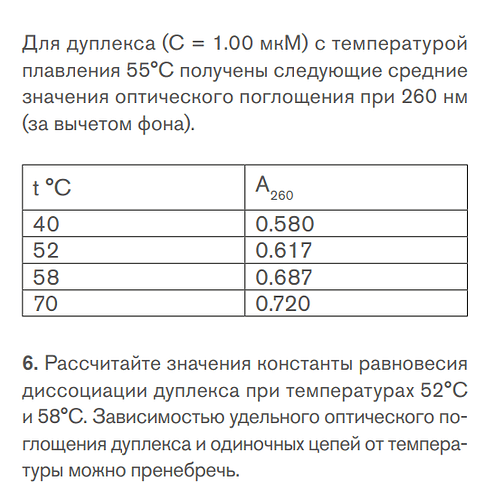
При температуре плавления значение константы равно одному. Поэтому мне кажется, нам дали значения поглощения при \pu{40^\circ C} и \pu{70^\circ C}, чтобы мы могли принять, что в первом случае в растворе присутствует только дуплекс, а во втором — только отдельные цепочки. В таком случае можно из выражения для оптической плотности найти значения \varepsilon_\text{AB}, \varepsilon_\text{A} и \varepsilon_\text{B} (наверное можно принять, что у обеих цепей коэф. поглощения равный).
A_{260}(\pu{40^\circ C}) = \varepsilon_\text{AB} \cdot 10^{-6} \cdot l
A_{260}(\pu{70^\circ C}) = 2 \ \varepsilon_\text{A} \cdot 10^{-6} \cdot l
При этом значение l они, наверное, дали ранее в задаче.
Я полагаю, что значения поглощения — величины складывающиеся, потому что можно мысленно представить поглощения раствора при \pu{40^\circ C} (когда есть и дуплекс и отдельные цепи), как два поочередных поглощения — сначала через раствор, где есть чистый дуплекс, а потом через раствор цепей. Поэтому при \pu{52^\circ C} можно записать так:
A_{260}(\pu{52^\circ C}) = \varepsilon_\text{AB} \cdot [\text{AB}] \cdot l + 2 \ \varepsilon_\text{A} \cdot (10^{-6} - [\text{AB}]) \cdot l
Из этого уравнения можно найти [\text{AB}], а потом и [\text{A}], и потом саму константу равновесия.
Ответ вышел неправильный , но в последнем уравнение у тебя мне кажется коэффициенты у двух распаренных участка ДНК будут разные
Можешь отправить полностью задачу с ответами? Возможно в начале есть какие-то слова, которые помогут в решении
Вот ответы K(52) = 9.49∙10-8; K(58) = 2.48∙10-6
Выходят те же ответы. Поскольку l не дано в явном виде, можно использовать значение 1см:
При отсутствии других указаний в частной фармакопейной статье
измерение оптической плотности проводят при указанной длине волны с
использованием кюветы 1 см
Взято отсюда
Найдем \varepsilon_\text{AB}:
A_{260}(\pu{40^\circ C}) = 0.580 = \varepsilon_\text{AB} \cdot 10^{-6}
\varepsilon_\text{AB} = \pu{5.8 \cdot 10^{5} M-1 cm-1}
Найдем \varepsilon_\text{A}:
A_{260}(\pu{70^\circ C}) = 0.720 = 2 \ \varepsilon_\text{A} \cdot 10^{-6}
\varepsilon_\text{A} = \pu{3.6 \cdot 10^{5} M-1 cm-1}
Из последнего уравнения в моем первом ответе выразим [\text{AB}]:
[\text{AB}] = \frac{ A_{260}(\pu{52^\circ C}) - 2 \ \varepsilon_\text{A} \cdot 10^{-6} }{ \varepsilon_\text{AB} - 2 \ \varepsilon_\text{A} } = \pu{7.357 \cdot 10^{-7} M}
[\text{A}] = 10^{-6} - [\text{AB}] = \pu{2.643 \cdot 10^{-7} M}
Здесь я взял на одну значащую цифру больше, на всякий.
Подставим в выражение для константы и получим ответ:
K(\pu{52^\circ C}) = \frac{ (2.643 \cdot 10^{-7})^2 }{ 7.357 \cdot 10^{-7} } = \pu{9.49 \cdot 10^{-8}}
6 лайков