Помогите пожалуйста решить задачу из савченко
7.1.14* Между двумя закрепленными зарядами в точке A отпускают частицу с зарядом q. Расстояние AB эта частица проходит за время t. За какое время
пройдет это же расстояние частица с зарядом 3q, если ее отпустить в точке A?
Массы частиц одинаковы
Есть идея записать систему диффуров, но решить ее затрудняюсь. Можете подсказать какой-нибудь более подходящий метод решения?
Хм, но ведь достаточно свести одну систему к другой системе, какой-нибудь заменой красивой.
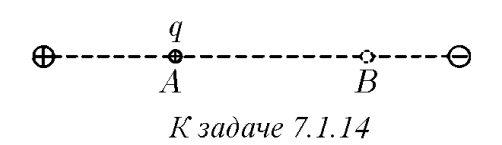
Делать дифференциальные уравнения не надо. Задача решается через методы подобия и размерностей.
Одна система по сути подобна другой. Параметры системы которые нужны для решения: линейные размеры (м), “временные размеры” (с)
Если линейные размеры увеличить в два раза, то все расстояния увеличатся в два раза. Если временные размеры увеличить в два раза то все отрезки веремени увеличатся в два раза.
Во второй системе где заряд другой, линейные размеры не поменялись, а вот временные изменились.
Надо заметить что в любой точке системы 1, в системе 2 ускорение частицы будет в 3 раза больше из-за заряда.
Ускорение это \frac{m}{s^2}
Оно комбинация линейных и временных размеров. Так как линейные размеры не поменялись, то чтобы ускорение увеличилось в 3 раза надо чтобы временные размеры уменьшились в \sqrt{3} раза:
3 \frac{m}{s^2}=\frac{m}{(s/\sqrt{3})^2}
Получатется ответ: t_1=\frac{t}{\sqrt{3}}
(Тут m это метры, s это секунды)
У них ответ наоборот, время увеличилось в \sqrt{3} раза, что вообще не логично. Сила везде увеличилась и время должно уменьшаться. Думаю у них не верно.
Чтобы лучше понять такой метод подобия рекомендую посмотреть задачу “кубик в кубике” из второго сезона Кубка ЛФИ 2021.
Вообще задачу можно было решить и по другому, более подгонному но логичному методу. Время прохождения в системе зависит от силы, массы, и расстояния. Если выразить время через эти велечины, то чтобы размерности совпадали надо:
t=\sqrt{\frac{mL}{F}}
Отсюда можно понять что если сила увеличится в три раза то время уменьшиться в \sqrt{3} раза
