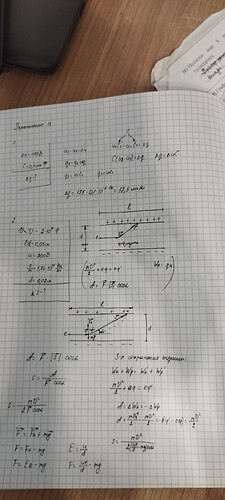
В пространство между пластинами плоского конденсатора влетает электрон со скоростью 2×10⁷м/с, направление которой парралельно пластинам. На какое расстояние сместится электрон за время движения внутри конденсатора, если длина его равна 0.05м и разность потенциалов равна 200В? Расстояние между пластинами конденсатора равно 0.02м. Отношение заряда электрона к его массе равно 1.76×10¹¹Кл/кг
Я попробовал решить задачу, но уперся в косинус угла между силой и вектором перемещения.
- силой тяжести по сравнению с электростатической в большинстве случаев можно пронебречь
- Попробуй решить методом динамика + кинематика. Аналогия с движением в поле тяжести (кажется так проще)
1 лайк
- У вас ошибка в ЗСЭ, там конечная кинетическая далеко не ноль. Она увеличивается
- cos ищется очень просто, cos\alpha=\frac{\Delta y}{s}, где \Delta y - искомое отклонение. ещё у вас на чертеже 2 разных угла обозначены \alpha, что странно, если что я написал выражение сos \alpha для угла между силой Кулона и перемещением
- @Batyrhan_Sheruen прав, через кинематику + динамику решать легче. Потому что, в случае с энергией тяжело(а может я дурачок) найти изменение кинетической энергии, ну типа она находится через работу, а вы выражаете перемещение через работу и получается замкнутый круг, плюс не понятно как связать всё это с длиной конденсатора.
- ещё мне кажется вы не очень понимаете условие задачи(судя по чертежам), вроде как в задаче просят найти отклонение электрона по вертикали за это время, и там из-за достаточно большой скорости он успеет пролететь через конденсатор до удара о его стенку.
Спасибо
Но как решать через динамику и кинематику?
1 лайк
\vec{F} = m\vec{a}, а дальше баллистика, где ты подставляешь \vec{a} вместо \vec{g}.
На самом деле так может быть даже легче. Изменение кинетической энергии можно найти по перпендикулярной к пластинам составляющей скорости, которую несложно вычислить, используя ускорение.
Единственное, что очень важно понять, так это то, что на работу влияет только перемещение, параллельное направлению силы. Это выходит из того, что A = F × s\cos{\alpha}, где s\cos{\alpha} по сути является проекцией вектора перемещения на вектор силы.
Уже отправили решение через кинематику, так что попробуй ещё решить эту задачу через энергию.
1 лайк