Плазма человеческой крови замерзает при −0,56 ◦C. Каково её осмотическое давление при 37 ◦C, измеренное с помощью мембраны, проницаемой только для воды?
О т в е т. π = 7,7 атм
Помогите решить задачу, нету никаких идей как бы к ней подступится, тяжкая глава
Как думаешь зачем тут дано изменение температуры замерзания?
мб, чтобы юзать PV=nRT ? просто нету криоскопической и эбулоскопическиой константы.
А так вот в чем проблема. Автор задачи тут имеет в виду кровь рассмотреть как раствор воды, что в теории, если судить по плотности, не так далеко от правды. Так что криоскопическую константу можешь взять как 1.86
ок, щас попытаюсь
Ну, че как там с задачей?
оооооооой, чет я забыл про нее пытался решить вроде что-то получалось, но потом пришлось уйти и забыл.
У меня выходит 7,658атм, как думаете, норм?
Да, у меня такой же ответ
можете пожалуйста показать свое решение, я все такие не смог решить
Понижение температуры замерзания описывается формулой:
Где m - моляльность раствора, а K_{кр}- криоскопическая константа, равная 1,86 K *kg/liter
Отсюда ты сможешь найти моляльность раствора. Но как найти осмотическое давление? Для нее надо знать молярность раствора, которая измеряется в, сам наверное знаешь, в mol/liter. В данном случае эти две величины равны, так как плотность воды 1 грамм на сантиметр куб. Либо просто подумай, есть ли большая разница между одним литром и одним килограммом воды?
Дальше остается лишь подставить значения в формулу для расчета осмотического давления
P = c * R* T
Как мы нашли криоскопическую константу, почему она равна 1,86 можете обьяснить?
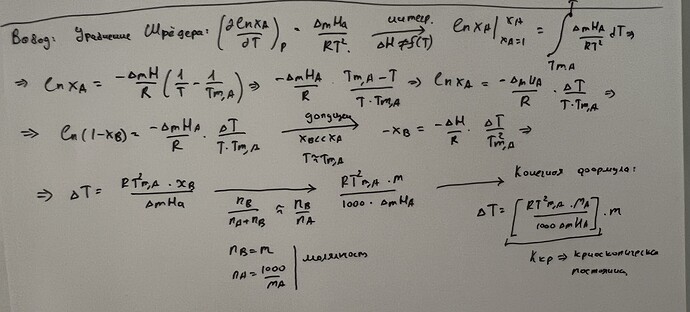
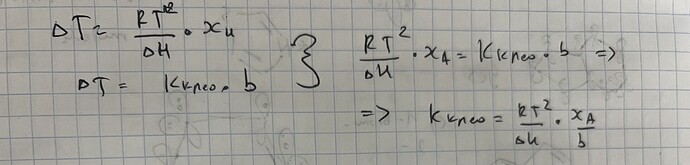Ну, сперва представим систему, в которой вода существует в виде льда и жидкости при 1 атм и температуре T_о (273.15 К). Думаю довольно справедливо сказать, что \Delta_{пл}G(T_о) = 0. Представим что мы растворили некоторое количество вещества В в этой системе, и тогда равновесное состояние в этой системе при таком же давлении 1 атм достигается при температуре T. Напишем выражение для химического потенциала жидкой воды при этих условиях:
Стоит отметить, что \mu_\ce{A}(ж,T) = \mu_\ce{A}^*(тв, T) (вспомним про равновесие), тогда
Пока что мы принимаем за данность то, что T < T_о. Поскольку x_А < 1, \Delta G_{пл}(T) > 0, что довольно логично, если посмотреть на фазовую диаграмму воды (давление мы принимаем за константу, и тогда по фазовой диаграмме видно, что при температуре T < T_о термодинамически стабильной фазой воды является лед). Если \Delta_{пл}G(T_о) = 0, то довольно справедливо, что \displaystyle \frac{\Delta_{пл}G(T_о)}{RT_о} = 0. В таком случае,
Поскольку выражение для химического потенциала выводится с помощью закона Рауля (который справедлив только для случаев, когда в систему было добавлено очень маленькое количество вещества В), можно сказать, что новая температура плавления не должна сильно отличаться от нормальной температуры плавления, а посему можно допустить, что изменения энтальпии и энтропии плавления не зависят от температуры в рассматриваемом случае.
Раз уж новая температура плавления не сильно отличается от нормальной, то T_оT \approx T_о^2. Также, поскольку x_А = 1 - x_В, можно в конечном итоге придти к следующему выражению:
Поскольку x_В довольно близка к нулю, можно использовать локальную линейную аппроксимацию. Рассмотрим график функции f(x_В) = \ln (1-x_В) и касательную в точке x_B = 0:
И наконец, \displaystyle m_В = \frac{n_В}{m_{\ce{H2O}}} = \frac{n_В}{n_{\ce{H2O}}}\cdot \frac{1}{M(\ce{H2O})}. Так как вещество В находится в очень маленьком количестве, \displaystyle x_В = \frac{n_В}{n_В + n_{\ce{H2O}}} \approx \frac{n_В}{n_{\ce{H2O}}}. В конечном итоге,
Если подставить необходимые данные, то вроде как должно получиться значение 1.86 для криоскопический константы для воды.
Она обычно будет даватся в заданиях как справочные данные но еремин в теормате их не любит давать и не давал особо но можно еще вывести этой формулой :
Как вы брали \Delta T? У меня он -37,56К, хотя в таком случае задача не выходит. Даже если брать \Delta T как 37,56К не выходит
