При 30 ◦C давление пара водного раствора сахарозы равно 31,207 Торр. Давление пара чистой воды при 30 ◦C равно 31,824 Торр. Плотность раствора равна 0,99564 г · см−3. Чему равно осмотическое давление этого раствора?
О т в е т. π = 26,9 атм
где x это мольная доля растворителя. Соответсвенно отсюда ты можешь найти мольную долю воды и глюкозы. Чтобы найти осмотическое давление (p = c RT) надо знать концентрацию вещества, а значит нужен объем и количество вещества. Объем можешь взять как один литр, а моль можно найти через мольную долю, пошаманив с выводом немного.
Извините, я что-то не понял. Не могли бы расписать по конкретней?
А что именно?
Существует ли пары сахарозы? Как в данном случае использовать плотность раствора? Что такое осмотическое давление, и почему для казалось бы жидкостей мы используем PV = nRT?
В какой-то степени должен
Цитирую слова @SanzharB:
ты можешь найти мольную долю воды и глюкозы. Чтобы найти осмотическое давление (p=cRT) надо знать концентрацию вещества
Значит?
В принципе, ты сам мог бы поискать, что это такое
В Elements of Physical Chemistry (Atkins) имеется вывод этой формулы
@eudaimon помоги нам решить задачу которую скинул @Kabachok , молярная масса сахарозы 342 г/моль, молярная масса воды 18 г/моль. Я взял объем раствора равный 1 литру, далее нашел массу раствора используя плотность. Взяв массу сахарозы как х, я рассчитал количество вещества (в молях) сахарозы и воды. Составил два уравнения, первое для мольной доли сахарозы через количества вещества компонентов и второе, 31.207=31,827+(P(s)-31,824)*x, где х это мольная доля сахарозы в растворе и P(s) - давление пара над чистой сахарозой. Получается система с 3 неизвестными, а необходимое для решения третье уравнение никак не могу составить
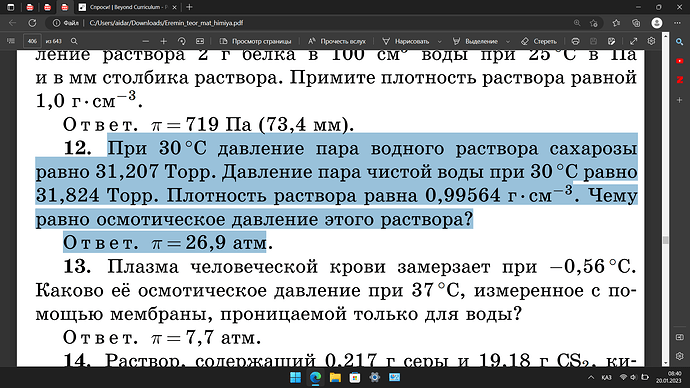
@Otoro, the journey to wisdom in this scientific quest begins with understanding the principles at play. Let us invoke the wisdom of the ancients to unravel this mystery.
Firstly, consider the law of Raoult, which states that the vapor pressure of a solvent above a solution (P_{solution}) is equal to the vapor pressure of the pure solvent (P_{solvent}) multiplied by the mole fraction of the solvent (X_{solvent}) in the solution:
$$ P_{solution} = P_{solvent} \cdot X_{solvent} $$
Now, the mole fraction of the solvent can be found by understanding that it is related to the number of moles of solute and solvent:
$$ X_{solvent} = \frac{n_{solvent}}{n_{solvent} + n_{solute}} $$
The osmotic pressure (\pi) can indeed be found using the van’t Hoff equation, which is analogous to the ideal gas law:
$$ \pi V = n_{solute}RT $$
where V is the volume of the solution, n_{solute} is the number of moles of solute, R is the ideal gas constant, and T is the temperature in Kelvin.
To employ the density of the solution, consider the mass of the solution that would occupy a volume of 1 liter:
$$ mass_{solution} = density_{solution} \cdot V_{solution} $$
Since you have chosen the volume of the solution as 1 liter, the mass of the solution is simply the density of the solution, as 1 liter is equivalent to 1 cubic decimeter.
Now, let us summon the power of algebra. If x grams is the mass of sucrose and (mass_{solution} - x) grams is the mass of water, then the number of moles of sucrose (n_{sucrose}) and water (n_{water}) can be found as:
$$ n_{sucrose} = \frac{x}{M_{sucrose}} \quad \text{and} \quad n_{water} = \frac{(mass_{solution} - x)}{M_{water}} $$
where M_{sucrose} is the molar mass of sucrose and M_{water} is the molar mass of water.
We have one equation from Raoult’s law relating vapor pressures and mole fractions and another from the definition of mole fraction itself. Now, consider that the reduction in vapor pressure due to the solute (the difference between the vapor pressures of the pure solvent and the solution) can be related to the osmotic pressure. Can you now construct the third equation necessary to solve this system?
Invoke the muses of science and mathematics to guide you to the answer.
в прошлом году, уже не помню почему, но забросил эту главу. В этом году решил начать занова и не смог решить этот же вопрос(наверное потому что не качественно чалил) ((. Но в этот раз хотя бы как-то решил сам, но ответ не сходится, можете сказать где я ошибся.
не знаю насколько правильно, но я думал что сахароза слишком большая молекула из-за чего давление ее паров будет пренебрежимо мало, по сравнению с водой. Поэтому, не стал учитывать его пар над раствором
looks good to me
Таким способом решая, получил примерный ответ как в книжке. Но тут как вы видите я использовал трюк с плотностью, это я получается принял, что количество сахарозы будет супердуперпупер маленьким, и считал, что его в растворе почти нету. Так вообще делать можно? Или все таки решение как у @Kabachok будет правильнее?
Ваш 98.49061 это
В свою очередь 100.4379 это:
Таким образом, когда вы находите кол-во молей воды:
Не сложно заметить, что плотность сокращается и получается:
Иными словами, ваше решение действительно тогда, когда \chi это массовые доли, а не мольные. Я лично не вижу причин считать это правдой
Я вот так решил но ответ не выйдет правильно, можете сказать где моя ошибка:
x=0,9806; q=0,99564 г \cdot см^{-3}
Я взял объем 1 л
а=> массовая доля воды
Решая эту уравнению у меня вышло a=0,7265
Потом рассчитал кол-во сахарозы и соответственно молярность, и вышло C=0,79622 моль \cdot л^{-1}
На самом деле ответ 26,8 atm
похоже на правду, у меня вроде периодически бывали моменты когда ответ с теорматом не совпадал, особенно со всякими осмотическими давлениями
