Вроде бы в моем решении все правильно но ответы не сходятся
У нас есть формула для нахождения давления:
Где \rho у нас плотность. Нам известно концентрация г/л, можем найти молярную концентрацию через:c_m=\frac{c}{M_{(гемоглобин)}}
Подставляешь под формулу осмотического давления p=c_mRT=\frac{c}{M_{(гемоглобин)}}RT
Пожалуй, здесь больше нельзя использовать уравнение Вант-Гоффа (которое привел @DiasTaraz) для расчета осмотического давления. Необходимо использовать вириальные коэффициенты, поскольку гемоглобин обладает многочисленными межмолекулярными взаимодействиями, что отклоняет раствор от идеальности. Вспомним как выглядит формула для расчета давления в случае реальных газов :
Отсюда видно, что зависимость осмотического давления от концентрации гемоглобина будет выглядеть следующим образом :
Пока мы не построим график зависимости высоты столбика раствора от концентрации гемоглобина , будет бессмысленно рассуждать. Осмотическое давление рассчитывается исходя из расчета такого гидростатического давления, которое будет компенсировать всевозможное влияние разных факторов на химический потенциал чистого растворителя и раствора так, что химические потенциалы последних сравняются. Думаю, отсюда понятно, что P_{osmotic}=ρgh , и тогда зависимость будет выглядеть следующим образом :
Поскольку в условии дали концентрацию гемоглобина в г/л, зависимость преобразуется в такой вид :
А теперь, перейдем к самому главному и интересному (а именно, к способу решения задачи). Мы знаем, что при определенных условиях, можно пренебрегать какими-то вириальными коэффициентами. Значит, наша задача состоит в том, чтобы построить график зависимости так, чтобы по свойству графика (прямая линия, парабола, гипербола, да хоть что угодно) мы могли определить, какими коэффициентами мы можем пренебрегать.
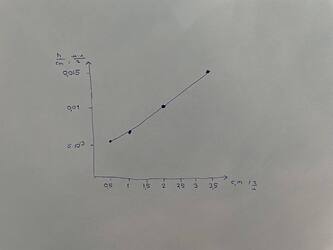
Отсюда довольно логично построить график зависимости \frac{h}{c_{m}} от c_{m} , поскольку так мы можем получить прямую линию, параболу, кубическую параболу, и.т.д) :
Если построить график, то мы получим следующую картину :
Отсюда видно, что график - линейный, и что это значит ? Правильно,. можно пренебречь всеми вириальными коэффициентами, кроме B, и тогда искомое уравнение зависимости будет выглядеть следующим образом :
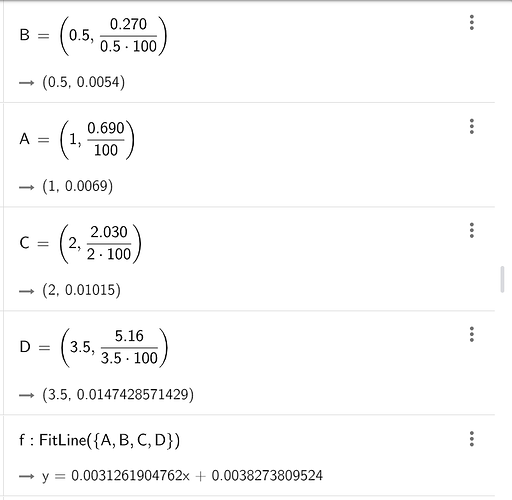
Все что нам остается сделать, так это найти intercept этой функции, и оттуда найти молярную массу гемоглобина. А сделать это можно с помощью графика, либо какими-то методами для расчета отклонений. У меня вышло, что intercept = \frac{RT}{ρgM} =3.842 \cdot 10^{-3}
В итоге M=\frac{8.314 \cdot 293}{3.842 \cdot 10^{-3} \cdot 999.8 \cdot 10^{-3} \cdot 9.8} =64711.4 г/моль = 64.7 кг/моль, что вроде бы совпадает с ответом
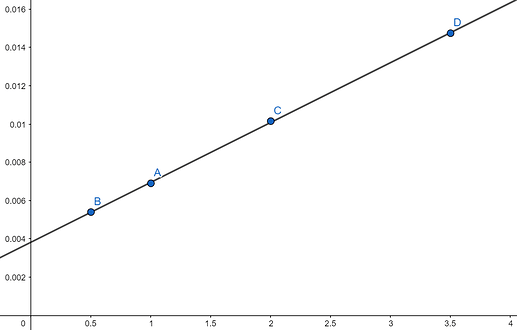
Я построил line of best fit на Geogebra и получил y-intercept при x=3.827 \cdot 10^{-3}. Тогда масса выйдет 64.97 кг, поэтому твое решение, скорее всего, верно.
Можете пожалуйста объяснить как у вас вышло 3,842•10^-3
Я решаю график следующим образом
У меня выходит 0,3827
Ты на метр походу забыл поделить значения