Я понял как мы вывели это уравнение:
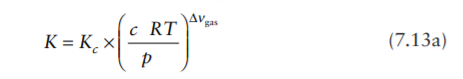
Но что мы сделали чтобы получить это:
???
Просто поделили газовую постоянную на давление, которое равно 1 бар (100 кПа). Тогда и получится что
K = K_{c} \cdot(\frac{T}{12.027})^{\Delta v_{gas}}
Заметим, что \frac{8.314}{100} = 0.08314 = \frac{1}{12.027}
5 симпатий
Стоп, а почему здесь килопаскали, а не паскали?
1 симпатия
Паскаль используют когда объем берут в m^3(так как J=Pa\cdot m^3), в данном случае единицы измерения молярной концентрации \frac{mol}{L}, видно что они взяли объем в литрах, если объем в литрах то давление в килопаскалях
3 симпатии
Спасибо.
Немного подробнее об этом. Удобно всегда использовать единицы измерения СИ — если все значения подставишь в СИ, можешь не волноваться о том, что у тебя получится на выходе — ответ будет в СИ.
Если взять значение R = 8.314, то мы сразу ставим конкретное ограничение — здесь R измеряется в \pu{Pa * m3 * K-1 * mol-1}. Что будет если в уравнение все подставлять в СИ?
\left[ \frac{cRT}{p} \right] = \frac{\pu{mol}}{\pu{m3}} \cdot \frac{\pu{Pa * m3}}{\pu{K * mol}} \cdot \frac{\pu{K}}{\pu{Pa}}
Видно, что все сокращается и результат — безмерное значение. Но если мы захотим \pu{m3} в концентрации поменять на \pu{L}, получится следующее (единицы измерения по центру мы не можем поменять, потому что уже взяли значение 8.314 для R. Если поменяем единицы измерения, то поменяется и значение константы):
\frac{\pu{mol}}{10^3 \pu{L}} \cdot \frac{\pu{Pa * m3}}{\pu{K * mol}} \cdot \frac{\pu{K}}{\pu{Pa}}
Значение уже не то, которое мы получали, подставляя все в СИ. Подставляя в \pu{mol m-3}, мы бы получили в 1000 раз меньшее значение, чем если бы мы подставляли в \pu{mol L-1}. (И получили бы уже не безмерную величину, а величину с измерением \pu{m3 L-1}) Чтобы скомпенсировать это изменение, можно поменять \pu{Pa} на \pu{kPa}.
\frac{\pu{mol}}{\pu{m3}} \cdot \frac{\pu{Pa * m3}}{\pu{K * mol}} \cdot \frac{\pu{K}}{\pu{Pa}} = \boxed{\frac{\pu{mol}}{10^3 \pu{L}} \cdot \frac{\pu{Pa * m3}}{\pu{K * mol}} \cdot \frac{\pu{K}}{10^{-3} \pu{kPa}}} = \frac{\pu{mol}}{\pu{L}} \cdot \frac{\pu{Pa * m3}}{\pu{K * mol}} \cdot \frac{\pu{K}}{\pu{kPa}}
То есть, мы не всегда можем такое проделать. В этом случае мы могли сделать так, потому что и объем и давление находились в знаменателе дроби. Если бы один из них находился в знаменателе, а другой — в числителе, такой фокус дал бы значение, в миллион раз отличающееся от того, которого мы бы получили, подставляя все в СИ.
3 симпатии