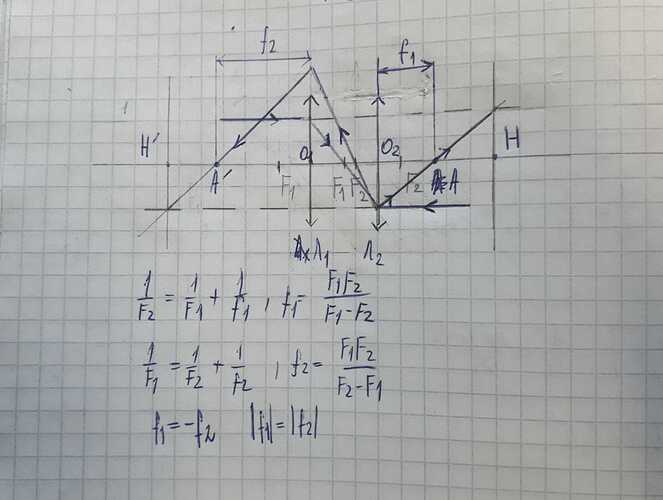
Две тонкие линзы с фокусными расстояниями f1 и f2 находятся на расстоянии L друг от друга, образуя центрированную систему. Найти фокусное расстояние f этой системы, также положения её главных плоскостей.
Можете обьяснить что тут главная оптическая плоскость. Думаю это положение линзы которым можно заменить систему из двух линз.
2 лайка
советую почитать 11 параграф в 4 томе Сивухина.
Две сопряжённые плоскости, отображающиеся друг в друга с поперечным увеличением y'/y=1, называются главными плоскостями оптической системы.
Таким образом, если ты пустишь луч параллельно оптической оси и найдешь пересечение продолжения этого прямого луча с лучом, получившимся после прохождения через систему линз, то ты получишь точку на главной плоскости оптической системы, из которой сможешь найти саму плоскость так как она перпендикулярна главной оптичесокй оси. (плоскостей будет две, потому что ты можешь пустить луч с двух сторон (слева и справа))
2 лайка
.
Можете помочь что мне сделать чтобы можно было найти расстояния главных плоскостей системы от точек О1 и О2.Не уверен но наверное тут надо заменить систему линз эквивалентной им линзой фокусное расстояние которого нам известно?
Можете помочь что мне сделать чтобы можно было найти расстояния главных плоскостей системы от точек О1 и О2.Не уверен но наверное тут надо заменить систему линз эквивалентной им линзой фокусное расстояние которого нам известно?
К сожалению, я не особо понял ход лучей на твоем рисунке.
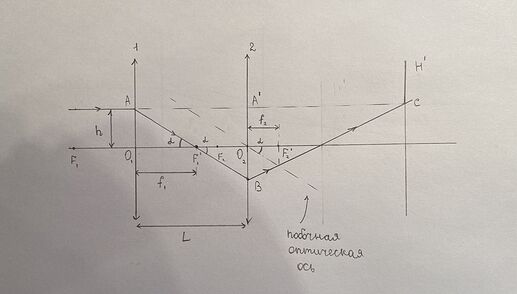
Для луча параллельного главной оптической оси рисунок хода луча будет примерно такой:
Ты можешь определить расстояние до главной оптической плоскости из этого рисунка
Спойлер
Из рисунка можно определить, что \displaystyle \tg(\alpha)=\frac{h}{f_1}, откуда расстояние \displaystyle O_2B = \frac{L-f_1}{f_1}h. Далее, для дальнейшего хода луча можно получить, что наклон луча ВС будет \displaystyle \tg(\beta) = \frac{h(L-f_1-f_2)}{f_1 f_2}. Отсюда ты сможешь найти расстояние \displaystyle O_2H' = \frac{Lf_2}{L-f_1-f_2}. Для другой оптической плоскости расстояние находится аналогично.
11 лайков
Мне хотелось бы узнать как полезно знать положение главной плоскости. Когда это будет необходимым для решения задачи?
1 лайк
Главные плоскости удобны при построении изображений центрированной оптической системы. То есть если луч входит в систему, то после её прохождения он будет выходить из точки главной плоскости на том же уровне, где луч вошел в систему через другую главную плоскость. Таким образом, главные плоскости помогают нам представить систему линз в виде одной толстой линзы.
7 лайков