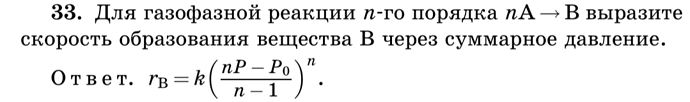3 лайка
Для 33 задачи
Судя по ответу, P - это и есть суммарное давление, а P_{0} - это начальное давление \ce{A}. Предположим, что прореагировало какая-то доля в-ва \ce{A}, скажем, \alpha. Тогда суммарное давление составит P_{0}-P_{0} \alpha + \frac{P_{0} \alpha}{n} = P. Исходя из закона действующих масс,
r_{B} = k(p_{A})^{n}
Из предыдущего уравнения, выразим альфу через суммарное давление, и получим
P_{0}n - P_{0}n \alpha + P_{0} \alpha = Pn
\alpha = \frac{Pn-P_{0}n}{P_{0}-P_{0}n}
Отсюда понятно, что p_{A} = P_{0} - P_{0} \alpha = P_{0} - \frac{Pn-P_{0}n}{1-n} = \frac{P_{0}-P_{0}n-Pn+P_{0}n}{1-n} = \frac{P_{0}-Pn}{1-n}
Следовательно,
r_{B} = k(\frac{P_{0}-Pn}{1-n})^{n}
Если поменять знаки местами, ничего не изменится, и получится также, как и в ответе.
10 лайков
Для задачи 8
Механизм бимолекулярный, поэтому справедливо следующее выражение :
r = kp(\ce{NO2})p(\ce{CO})
Далее, по условию, температура у нас постоянная, и давление фиксированное. Поэтому можно утверждать, что p(\ce{NO2})+p(\ce{CO}) = const. Пусть соотношение реагентов будет неким x (соотношение диоксида азота к монооксиду углерода), тогда xp(\ce{CO})+p(\ce{CO)}= const ; p(\ce{CO)}=\frac{const}{1+x} , значит p(\ce{NO2}) = \frac{x \cdot const}{1+x}.
Теперь, запишем модифицированный закон действующих масс :
r = k\frac{const^{2} \cdot x}{(1+x)^{2}} = const' \cdot \frac{x}{(1+x)^{2}}
где const' = k \cdot const^{2}
Половина задачи уже решена, и теперь остается задуматься, что означает наибольшая скорость ? Это означает, что произведение парциальных давлений \ce{NO2} и \ce{CO} максимальное. Получается, нам надо взять производную (т.е. скорость изменения произведения парциальных давлений от x) и приравнять к нулю. Это логично, потому что когда произведение достигает максимума, бесконечно малое изменение этого произведения равно нулю, т.к. она не возрастает, и не убывает. (далее, обозначим произведение как П
\frac{П}{dx} = \frac{(1+x)^{2}-x(2x+2)}{(1+x)^{4}} = 0
(1+x)^{2}-x(2x+2) = 0
x^{2} + 2x + 1 - 2x^{2}-2x = 0
x = +1
На самом деле, там еще возможен ответ x = -1 , но отрицательное соотношение - это абсурд, поэтому я не стал его писать (простите, математики).
Вот так вот и оказалось, что наибольшая скорость (начальная) достигается тогда, когда соотношение равно 1:1
Теперь, думаю тебе понятно как найти второе соотношение
(вообще, лучше было бы создать две разные темы на эти задачи)
14 лайков
Спасибо огромное
1 лайк
извините, но я не понял как найти его, может кто-нибудь показать ?
думал все до момента перед тем брать производную будет одинаковым, но вместо r максимальный мы берем rmax/10, потом десятку перекидываем на ту сторону и решаем опять также приравняв к нулю, но у меня чота не выходит, кстати уравнение следующее
10 \cdot (1+x)^2-20x(1+x)
отсюда оба корня выходят отрицательными
1 лайк
В этой задаче, в данном случае вы математический доказали, что наибольшая скорость будет достигнута, именно когда у нас соотношение 1:1. Данный трюк работает всегда и везде независимо от ситуации? (случай, когда у нас только 2 реагента)
А почему p_{\ce{NO2}}+p_{\ce{CO}}=\text{const} ? Почему из фиксированного давления следует вот это?
1 лайк
Типа их сумма всегда будет постоянной
Не могу понять почему так(
1 лайк
Это кжс не верно, т.к по мере реакции реагенты будут тратится и соответственно их давление будет падать. Давление поддерживается постоянным имеют ввиду общее давление, а не давление реагентов
Перечитал свой ответ, и понял, что задачу можно было решить гораздо эффективнее в плане времени. Для этого надо было всего лишь использовать закон Дальтона. Раз уж давление в системе постоянное,
r = kp_{\ce{NO2}} p_{\ce{CO}} = k(px)(p(1-x)) = kp^2 \cdot x (1-x)
Далее, вся задача просто сводится к типичной задаче на применение производных. Нам буквально надо лишь найти критическую точку функции f(x) = x-x^2, показать что это соответствует максимуму, а затем найти некоторую точку x_0, при которой f(x_0) = \dfrac{f_{max}}{10}.
7 лайков