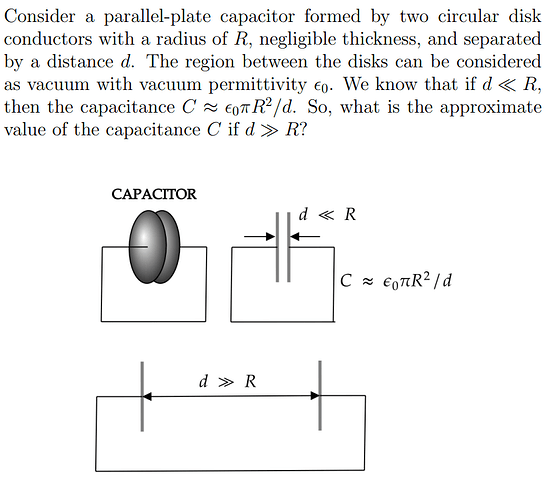
A problem I wanted to share. From capacitors, translated by me.
The capacitance is by definition C=q/U. You can find an electric field E(x) at the distance x from the positively charged disk at its axis, and integrate U=-\int_+^- Edx.
5 лайков
Solution method: When d>>R, each capacitor plate can be considered individually. Determine if a circular conductive disk of radius R is charged Q, then what will be the charge distribution on it, from there calculate the potential energy V, and finally the capacitance of these two circular disks can be calculated according to C= Q/2V.
1 лайк
Well, as far as I remember, the charge distribution for an isolated disk is
\sigma(r) = \frac{Q}{4\pi R^2}\left(1-\frac{r^2}{R^2}\right)^{-\frac{1}{2}},
and it is obtained through considering the disk as a special case for a conductive ellipsoid. But we are free to provide an approximate answer, so considering the charge distribution is not really necessary. I guess you can even think of those capacitors as point charges and use the parameter R as an acceptable lower limit when integrating for the potential difference.
5 лайков
Yes. You are correct, my friend.
5 лайков
I’ll share another (more challenging) problem today. Hopefully, the community will enjoy that. Its been a long time since I’ve been here.
1 лайк