F(r) сила взаимодействия между шариками (заряженный и незаряженный)

Физика Электромагнетизм
1

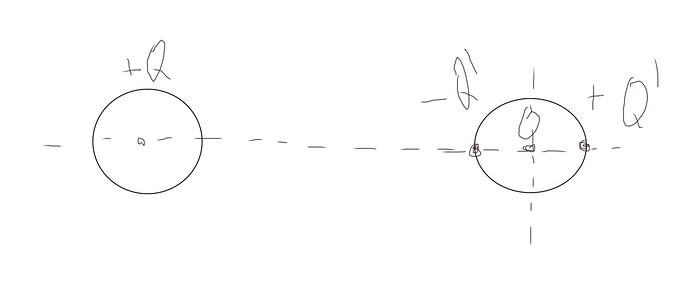
Как меняется с расстоянием r сила взаимодействия F между двумя маленькими шариками из которых один заряжен другой нет

2

Ответ у меня есть, его я тебе не дам. Вместо него дам три наводящих вопроса:

  1. Чему равны массы шариков?
  2. Между чем возникает электростатические взаимодействия (силы)?
  3. Сделаны ли шарики из металла?
3 лайка
3

также в задаче нужно знать размеры шариков и материал (вероятно предполагается, что это металлические шарики, однако по условию это не понятно)

2 лайка
4

В условие не даны не массы шариков не размеры не материал.

5

Между шариками появляется сила из за того что под действием поля первого шарика у второго появляюся макроскопические заряды

1 лайк
6

Шарики металлические?

7

В задаче не написано. Но скорее всего да

8

Да, металлические. Нам недавно кстати такую же прям задачу давали. Здесь через напряжённость просто решается. Но если честно, мне это задача не оч красивой кажется

9

Можно тогда условие задачи?

@Amir в смысле давали? Это откуда-то с урока или это олимпиада?

10

да, нам на уроке давали такую
хз может с какой-то олимпиады

11

Если можешь дай подсказку.

1 лайк
12

К примеру, выглядит так

Screenshot 2022-09-09 205454
Screenshot 2022-09-09 2054541932×838 38.3 KB

Решение

Крч, в авторском решении в точке O приравняли напряжённости полей и оттуда находят Q' , потом подставляется в закон кулона и находится сразу отношение сил. Силой притяжения по условию можно было пренебречь и тд

4 лайка
13

Все, спасибо!

2 лайка
14

Данную задачу можно решить еще другим способом

Решение

В предыдущем решении было сделано необоснованное предположение о расположении зарядов на концах сферы (хоть это и приводит к правильному ответу, но не дает причин не поставить эти заряды в другом месте, что приведет к неверной конечной формуле для силы).

Из-за того, что шарики маленькие (расстояние между ними много больше их радиусов) можно сказать, что поле заряженного шарика является однородным вблизи 2 шарика. Тогда данный шар поляризуется и будет представлять собой диполь, момент которого можно представить как p=4\pi \epsilon_0 r^3 E =\frac{Qr^3}{R^2}
(http://kvant.mccme.ru/pdf/2001/01/kv0101chern.pdf)

Тогда силу действующую на диполь можно найти как F=p \frac{dE}{dR}=\frac{Qr^3}{2\pi \epsilon_0 R^5}

7 лайков
15

Я кстати этот момент сам не особо понял и решил, что это просто из-за того, что R>>r

4 лайка