1 лайк
Просто всё запомнить из википедии. До некоторых можно догадаться логический по форме орбиталей. До некоторых нет.
Именно твой случай совпадает с плоским квадратом.
3 лайка
Есть теория кристаллического поля, где электроны расщепляются и попадают на эти орбитали:
d_{z^2},d_{x^2-y^2},d_{xy},d_{xz},d_{zy}
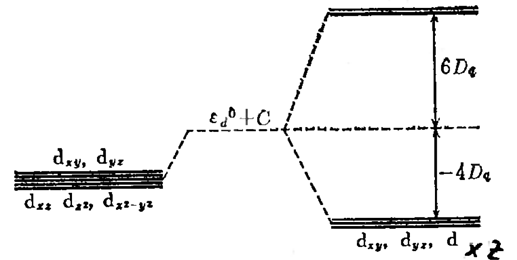
Как сказал @Baurzhan строение этого соединения плоский квадрат. Можно задать вопрос: откуда эта ранжировка орбиталей? Можно рассмотреть теорию кристаллического поля октаэдра, где электроны комплексных соединении расщепляются на наборы орбиталей t_{2g},e_g. t_{2g} имеет 3 d-орбиталей: d_{xy},d_{xz},d_{zy}, а e_g не стабильные:d_{z^2},d_{x^2-y^2}. Разница между энергиями этих двух орбиталей большая. В структуре октаэдра центральный атом металла окружён шестью лигандами, если, убрать два лиганда из z оси у нас появятся 2 пары электронов вместо лигандов и структура будет плоским квадратом. При удалении двух лигандов из z оси у нас d_{z^2} орбиталь стабилизируется и энергии d_{yz},d_{xz} орбиталей понижаются.
3 лайка
На плоский квадрат не похоже, там ведь yz выше, чем xz.
Кратко, в чем суть ТКП? Лиганды создают электростатическое поле, которое влияет на состояние центрального иона за счет электростатического отталкивания между электронами центрального иона и электронами лигандов. Расщепление энергий d-орбиталей будет разным в зависимости от формы поля. На диаграмме показаны свободный ион, ион в сферическом поле, ион в октаэдрическом поле и ион в поле в форме плоского квадрата. В первом переходе энергия повышается, потому что мы добавили лиганды — появилось электростатическое отталкивание. При этом энергии орбиталей одинаковые, потому что в сферическом поле лиганды одинаково действуют на все орбитали.
В октаэдре лиганды расположены на осях, поэтому наибольшее отталкивание будет с орбиталями d_{x^2-y^2} и d_{z^2}. Отталкивание уменьшится в случае орбиталей d_{xy}, d_{xz} и d_{yz}. Поэтому, первые орбитали повышаются в энергии, а вторые — понижаются. Если неясно, стоит посмотреть на то, как расположены d-орбитали в пространстве.
В переходе к плоскому квадрату лиганды убираются с z оси, поэтому орбиталь d_{z^2} сильно понизится, а d_{xz} и d_{yz} понизятся, но не так сильно. (Я немного неправильно изобразил в диаграмме.)
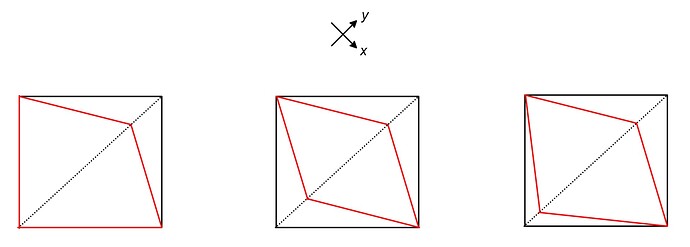
Я уже сказал, почему считаю, что в приведенной задаче ответ не плоский квадрат. В задаче d_{yz} стоит выше по энергии, чем d_{xz}, значит у d_{yz} больше отталкивания. Мне кажется, это может быть так, что взяли плоский квадрат и какой-то из лигандов на оси y приблизили к центральному иону. Вариантов может быть трое (указал ниже), но я бы выбрал ромб, потому что он симметричный. (Но я не уверен, что это наверняка так.)
А еще это могло быть не увеличение отталкивания по оси y, а уменьшение отталкивания по оси x. То есть, среди других вариантов можно было предложить и ромб, который был получен путем “растягивания” по x-оси.
6 лайков
Чтобы ответить на этот вопрос точнее. Обратимся к тому, как вообще высчитывают расщепление.
Простите меня, но тут будет много гадостной теории. Но зато некоторые узнают почему например \Delta_t=4/9\Delta_o
Чтобы узнать энергию в квантовой механике, необходимо решить уравнение Шредингера
\hat H| \psi \rangle = E| \psi \rangle
где
\hat{H} = \hat T+\hat V = -\frac{\hbar^2}{2m}\nabla^2 + \hat V =-\frac{\hbar^2}{2m}\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right) + \hat V
где
\hat H оператор Гамильтона
\hat T оператор кинетической энергии,
\hat V оператор потенциальной энергии
Если же ты изначально знаешь волновую функцию, то энергию можно найти как
E= \langle \psi |\hat H| \psi \rangle = \int \psi^* \hat H \psi \,dV \\
Но есть проблемы, оно обычно нифига руками не решается. Поэтому придется пользоваться приближениями. Этим и займемся. Cначала разберем пример для октаэдра.
Начальные приближения:
- Расстояния до центрального атома R
- Лиганды точечные заряды Q
На каждый электрон в центральном атоме начнет действовать дополнительный потенциал, поэтому к \hat V атома добавится еще -eU(x,y,z)
Кто помнит школьную программу, легко найдет вид U(x,y,z)
U(x,y,z)= \frac{Q}{4\pi\varepsilon_0} \biggl(
\frac{1}{\sqrt{\left(x-R\right)^2+y^2+z^2}}+
\frac{1}{\sqrt{\left(x+R\right)^2+y^2+z^2}}+
\\+
\frac{1}{\sqrt{\left(y-R\right)^2+x^2+z^2}}+
\frac{1}{\sqrt{\left(y+R\right)^2+x^2+z^2}}+
\\+
\frac{1}{\sqrt{\left(z-R\right)^2+y^2+x^2}}+
\frac{1}{\sqrt{\left(z+R\right)^2+y^2+x^2}} \biggl)
Конечно очень хочется это всё переписать в сферических координатах, но пощадите, попробуйте сами это сделать дома.
В общем у нас возникает проблема, на бумаге не решить уравнение Шредингера. Что будет делать? Есть какие-то упрощения? Да, и довольно много.
Первое, считать будем одноэлектронную волновую функцию (в общем будем считать, что орбитали существуют, да-да, это всегда было приближением, для тех кто не в курсе).
Второе, воспользуемся теорией возмущений.
О чём вообще речь, теория возмущений, это способ находить приблизительные решения для уравнения Шредингера, если какое-то решение мы уже знаем.
Например, если наш Гамильтониан можно представить как сумму
\hat H= \hat H_o + \hat V'
Где \hat V' это малое возмущение, и мы знаем решение для \hat H_o, обозначу за | \psi_o \rangle
То мы можем получить целый ряд приближений, но нас будет интересовать только энергия. Это первое приближение теории возмущений. Берут просто новый гамильтониан, а в формулу средней энергии подставляют старую известную волновую функцию
\begin{gathered}
E= \langle \psi_o |\hat H| \psi_o \rangle = \int \psi_o \hat H \psi_o \,dV =
\int \psi_o \left( \hat H_o + \hat V'\right) \psi_o \,dV =\\ = \int \psi_o \hat H_o \psi_o \,dV+\int \psi_o \hat V' \psi_o \,dV = E_o +\Delta E
\end{gathered}
Вот последний интеграл \int \psi_o \hat V' \psi_o \,dV и есть поправка к энергии
Если бы лигандов не было, то орбитальное одноэлектронное решение для центрального атома, можно было бы представить в виде слейторовских орбиталей (это водородоподобные одноэлектронные орбитали, с эффективным зарядом ядра, без узлов, т.е. 1s все 2p все 3d и т.д.)
А конкретно:
\begin{gathered}
\psi_{3d_{xy}} = \frac{\sqrt 2}{81 \sqrt \pi} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3} \sin^2 \theta \sin \varphi \cos \varphi \\
\psi_{3d_{yz}} = \frac{\sqrt 2}{81 \sqrt \pi} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3} \sin \theta \cos \theta \sin \varphi \\
\psi_{3d_{xz}} = \frac{\sqrt 2}{81 \sqrt \pi} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3} \sin \theta \cos \theta \cos \varphi \\
\psi_{3d_{x^2-y^2}} = \frac{1}{81 \sqrt {2\pi}} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3} \sin^2 \theta \left(\cos^2 \varphi - \sin^2 \varphi \right) \\
\psi_{3d_{z^2}} = \frac{1}{81 \sqrt {6\pi}} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3}
\left(3\cos^2\theta-1 \right)
\\
a_0=\frac{\hbar^2}{me^2} \\
\rho=\frac {Z^*r}{a_0}
\end{gathered}
Их мы возьмем как |\psi_o \rangle , а оператор возмущения у нас это -eU(x,y,z)
Попробуем найти изменение энергии для \psi_{3d_{z^2}}
\begin{gathered}
\Delta E = \int \psi_{3d_{z^2}}^* \hat V' \psi_{3d_{z^2}}\,dV
\end{gathered}
У нас возникает проблема, интеграл руками не берется. Для этого мы возьмем приближение для U(x,y,z)
Используем для этого разложение по Тейлору в начале координат до второй степени
\begin{aligned}
\mathrm{T}= x \dfrac {\partial} {\partial x}+ y \dfrac {\partial} {\partial y}+ z \dfrac {\partial} {\partial z}
\\
U(x,y,z)=\sum\limits_{k=0}^n \dfrac {\mathrm{T}^k U_0} {k!} + R_n(x,y,z),
\end{aligned}
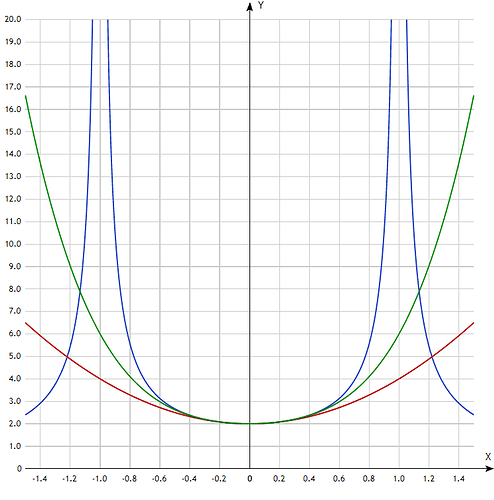
Всё старше четвертого порядка выкинем. Это должно хорошо помочь, например, для функции
f(x) = \frac {1}{\sqrt{\left(x+1 \right)^2}} + \frac {1}{\sqrt{\left(x-1 \right)^2}}
Разложение до второго и четвертого порядка, дает
\begin{gathered}
f(x) = 2+2x^2\\
f(x) = 2+2x^2 + 2x^4
\end{gathered}
Синее изначальная функция, красное и зеленое приближения
На графике отчетливо видно, что около нуля там очень хорошее попадание. А нам и нужно около нуля, т.к. электронная плотность у нас на центральном атоме
Я не буду издеваться над вами и сразу напишу что получается
U(x,y,z)= \frac{2Q}{4\pi\varepsilon_0R} \left[ 3 + \frac{35}{8R^4} \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \right]
Подставим в наш интеграл
\begin{gathered}
\Delta E_{3d_{z^2}} = -e\int \psi_{3d_{z^2}}^* \frac{2Q}{4\pi\varepsilon_0R} \left[ 3 + \frac{35}{8R^4} \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \right] \psi_{3d_{z^2}}\,dV
\end{gathered}
Скажу сразу, чтобы его взять, придется потратить немало внимательности и времени. Но кто хочет, тот попробует. А я для {3d_{z^2}} покажу
Спойлер
\begin{gathered}
\Delta E_{3d_{z^2}} = -\frac{2Qe}{4\pi\varepsilon_0R} \int \psi_{3d_{z^2}}^* \left[ 3 + \frac{35}{8R^4} \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \right] \psi_{3d_{z^2}}\,dV = \\
= -\frac{6Qe}{4\pi\varepsilon_0R} -\frac{2Qe}{4\pi\varepsilon_0R} \frac{35}{8R^4} \int \psi_{3d_{z^2}}^* \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \psi_{3d_{z^2}}\,dV
\end{gathered}
Нужно сделать замену декартовых координат на сферические
Для этого
\begin{gathered}
\begin{cases}
x=r\sin\theta\cos\varphi, \\
y=r\sin\theta\sin\varphi, \\
z=r\cos\theta.
\end{cases}
\\
\mathrm{d}V = \mathrm{d}x\, \mathrm{d}y\, \mathrm{d}z = J(r,\theta,\varphi) \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\varphi = r^2 \sin \theta \, \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\varphi
\end{gathered}
а еще удобно радиальную часть волновой функции вытащить отдельно, т.к. у всех d орбиталей она одинаковая
\psi_{3d_{z^2}} = \frac{1}{81 \sqrt {6\pi}} \left( \frac {Z^*}{a_0} \right)^{3/2} \rho^2 e^{-\rho/3}
\left(3\cos^2\theta-1 \right) = R_d(r)\sqrt{\frac{5}{16\pi}} \left(3\cos^2\theta-1 \right)
\\
Тогда
\begin{gathered}
\iiint \psi_{3d_{z^2}}^* \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \psi_{3d_{z^2}}\,dxdydz =
\\
=\frac{5}{16\pi} \iiint R_d(r)^2 \left(3\cos^2\theta-1 \right)^2 \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \,dxdydz =
\\=
\frac{5}{16\pi} \iiint R_d(r)^2\left(3\cos^2\theta-1 \right)^2 r^4
\left( \sin^4\theta\cos^4\varphi +\sin^4\theta\sin^4\varphi +\cos^4\theta -\frac3{5} \right)
r^2 \sin \theta \,dr d\phi d\theta = \\
= \frac{5}{16\pi} \iiint R_d(r)^2\left(3\cos^2\theta-1 \right)^2 r^4
\left( \sin^4\theta\cos^4\varphi +\sin^4\theta\sin^4\varphi +\cos^4\theta -\frac3{5} \right)
r^2 \sin \theta \,dr d\phi d\theta = \\
= \frac{5}{16\pi} \int\limits_0^\infty R_d(r)^2r^6\,dr\int\limits_0^{2\pi}\,d\phi \int\limits_0^{\pi}\sin \theta
\left(3\cos^2\theta-1 \right)^2 \left( \sin^4\theta\cos^4\varphi +\sin^4\theta\sin^4\varphi +\cos^4\theta -\frac3{5}\right)
\,d\theta =\\
= \frac{5}{16\pi} \int\limits_0^\infty R_d(r)^2r^6\,dr \cdot \frac{64\pi}{175} = \frac{4}{35}\int\limits_0^\infty R_d(r)^2r^6\,dr
\end{gathered}
Ну и
\begin{gathered}
\Delta E_{3d_{z^2}} = -\frac{6Qe}{4\pi\varepsilon_0R} -\frac{2Qe}{4\pi\varepsilon_0R} \frac{35}{8R^4} \int \psi_{3d_{z^2}}^* \left( x^4 +y^4 +z^4 -\frac3{5} r^4 \right) \psi_{3d_{z^2}}\,dV =\\
= -\frac{6Qe}{4\pi\varepsilon_0R} -\frac{2Qe}{4\pi\varepsilon_0R} \frac{35}{8R^4} \frac{4}{35}\int\limits_0^\infty R_d(r)^2r^6\,dr = -\frac{6Qe}{4\pi\varepsilon_0R} -\frac{Qe}{4\pi\varepsilon_0R^5}\int\limits_0^\infty R_d(r)^2r^6\,dr
\end{gathered}
Если ввести обозначения
\begin{gathered}
C=-\frac{6Qe}{4\pi\varepsilon_0R} \\
D_q= -\frac{Qe}{24\pi\varepsilon_0R^5}\int\limits_0^\infty R_d(r)^2r^6\,dr
\end{gathered}
То
\begin{gathered}
\Delta E_{3d_{z^2}} = С+6D_q
\end{gathered}
С оказалось поправкой для сферического поля.
Если сделать для всех d орбиталей расчет, то получим
\begin{gathered}
\Delta E_{3d_{xy}} = С-4D_q\\
\Delta E_{3d_{xz}} = С-4D_q\\
\Delta E_{3d_{yz}} = С-4D_q\\
\Delta E_{3d_{x^2-y^2}} = С+6D_q\\
\Delta E_{3d_{z^2}} = С+6D_q\\
\end{gathered}
А теперь давайте проверим, что за ромб нам нужно взять, чтобы у нас получилась такое странное распределение орбиталей по уровням. По оси x расстояние до лигандов пусть будет a, а по оси y b
Повторяем наши рассуждения
\begin{gathered}
U(x,y,z)= \frac{Q}{4\pi\varepsilon_0} \biggl(
\frac{1}{\sqrt{\left(x-a\right)^2+y^2+z^2}}+
\frac{1}{\sqrt{\left(x+a\right)^2+y^2+z^2}}+
\\+
\frac{1}{\sqrt{\left(y-b\right)^2+x^2+z^2}}+
\frac{1}{\sqrt{\left(y+b\right)^2+x^2+z^2}} \biggl)
\end{gathered}
Ряд тейлора до четвертого порядка, для этой штуки это
\begin{gathered}
U(x,y,z)= \frac{Q}{4\pi\varepsilon_0} \Biggl[
2 \left( \frac{1}{a}+\frac{1}{b} \right)+x^2 \left( \frac{2}{a^3}-\frac{1}{b^3}
\right)+ y^2\left( \frac{2}{b^3}-\frac{1}{a^3} \right) - z^2 \left( \frac{1}{a^3}+\frac{1}{b^3}
\right) + \\
+ x^4 \left( \frac{2}{a^5}+\frac{3}{4b^5} \right) + y^4 \left( \frac{2}{b^5}+\frac{3}{4a^5} \right) + z^4 \left( \frac{3}{4b^5}+\frac{3}{4a^5} \right) - x^2y^2 \left( \frac{6}{b^5}+\frac{6}{a^5} \right) - \\ -x^2z^2\left( \frac{6}{a^5}-\frac{3}{2b^5} \right)- y^2z^2\left( \frac{6}{b^5}-\frac{3}{2a^5} \right)
\Biggl]
\end{gathered}
Я надеюсь я нигде не ошибся, ибо место для ошибок тут просто целая куча
Делаем замену и считаем
\begin{gathered}
\Delta E_{3d} = -e\int \psi_{3d}^* \frac{Q}{4\pi\varepsilon_0} \Biggl[
2 \left( \frac{1}{a}+\frac{1}{b} \right)+x^2 \left( \frac{2}{a^3}-\frac{1}{b^3}
\right)+ y^2\left( \frac{2}{b^3}-\frac{1}{a^3} \right) - z^2 \left( \frac{1}{a^3}+\frac{1}{b^3}
\right) + \\
+ x^4 \left( \frac{2}{a^5}+\frac{3}{4b^5} \right) + y^4 \left( \frac{2}{b^5}+\frac{3}{4a^5} \right) + z^4 \left( \frac{3}{4b^5}+\frac{3}{4a^5} \right) - x^2y^2 \left( \frac{6}{b^5}+\frac{6}{a^5} \right) - \\ -x^2z^2\left( \frac{6}{a^5}-\frac{3}{2b^5} \right)- y^2z^2\left( \frac{6}{b^5}-\frac{3}{2a^5} \right)
\Biggl] \psi_{3d}\,dV = \\
=-\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) -\frac{eQ}{4\pi\varepsilon_0} \int \psi_{3d}^*\Biggl[
x^2 \left( \frac{2}{a^3}-\frac{1}{b^3}
\right)+ y^2\left( \frac{2}{b^3}-\frac{1}{a^3} \right) - z^2 \left( \frac{1}{a^3}+\frac{1}{b^3}
\right) + \\
+ x^4 \left( \frac{2}{a^5}+\frac{3}{4b^5} \right) + y^4 \left( \frac{2}{b^5}+\frac{3}{4a^5} \right) + z^4 \left( \frac{3}{4b^5}+\frac{3}{4a^5} \right) - x^2y^2 \left( \frac{6}{b^5}+\frac{6}{a^5} \right) - \\ -x^2z^2\left( \frac{6}{a^5}-\frac{3}{2b^5} \right)- y^2z^2\left( \frac{6}{b^5}-\frac{3}{2a^5} \right)
\Biggl] \psi_{3d}\,dV = \\
=-\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) -\frac{eQ}{4\pi\varepsilon_0} \int \psi_{3d}^*\Biggl[
x^2 \left( \frac{2}{a^3}-\frac{1}{b^3}
\right)+ y^2\left( \frac{2}{b^3}-\frac{1}{a^3} \right) - z^2 \left( \frac{1}{a^3}+\frac{1}{b^3}
\right) \Biggl] \psi_{3d}\,dV - \\ -\frac{eQ}{4\pi\varepsilon_0} \int \psi_{3d}^*\Biggl[ x^4 \left( \frac{2}{a^5}+\frac{3}{4b^5} \right) + y^4 \left( \frac{2}{b^5}+\frac{3}{4a^5} \right) + z^4 \left( \frac{3}{4b^5}+\frac{3}{4a^5} \right) -\\
- x^2y^2 \left( \frac{6}{b^5}+\frac{6}{a^5} \right) -x^2z^2\left( \frac{6}{a^5}-\frac{3}{2b^5} \right)- y^2z^2\left( \frac{6}{b^5}-\frac{3}{2a^5} \right)
\Biggl] \psi_{3d}\,dV
\end{gathered}
Найдем последний интеграл, только сначала
\begin{gathered}
\psi_{3d_{z^2}} = R_d(r)\sqrt{\frac{5}{16\pi}} \left(3\cos^2\theta-1 \right)
\\
\psi_{3d_{xy}} = R_d(r)\sqrt{\frac{15}{4\pi}} \sin^2 \theta \sin \varphi \cos \varphi
\\
\psi_{3d_{xz}} = R_d(r)\sqrt{\frac{15}{4\pi}} \sin \theta \cos \theta \cos \varphi
\\
\psi_{3d_{yz}} = R_d(r)\sqrt{\frac{15}{4\pi}} \sin \theta \cos \theta \sin \varphi
\\
\psi_{3d_{x^2-y^2}} = R_d(r)\sqrt{\frac{15}{16\pi}} \sin^2 \theta \left(\cos^2 \varphi - \sin^2 \varphi \right)
\end{gathered}
Посчитаем
\begin{gathered}
\Delta E_{3d_{z^2}} = -\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) +\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\left(\frac{1}{a^3}+\frac{1}{b^3}
\right) \int R_d(r)^2 r^4 \,dr -\frac{eQ}{4\pi\varepsilon_0}\frac{15}{7} \left(\frac{1}{a^5}+\frac{1}{b^5}
\right)
\int R_d(r)^2 r^6 \,dr
\\
\Delta E_{3d_{xy}} = -\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) -\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\left(\frac{1}{a^3}+\frac{1}{b^3}
\right) \int R_d(r)^2 r^4 \,dr +\frac{eQ}{4\pi\varepsilon_0}\frac{8}{21} \left(\frac{1}{a^5}+\frac{1}{b^5}
\right)
\int R_d(r)^2 r^6 \,dr
\\
\Delta E_{3d_{xz}} =-\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) -\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\left(\frac{1}{a^3}-\frac{2}{b^3}
\right) \int R_d(r)^2 r^4 \,dr +\frac{eQ}{4\pi\varepsilon_0}\frac{8}{21} \left(\frac{4}{a^5}-\frac{1}{b^5}
\right)
\int R_d(r)^2 r^6 \,dr
\\
\Delta E_{3d_{yz}} = -\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) +\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\left(\frac{2}{a^3}-\frac{1}{b^3}
\right) \int R_d(r)^2 r^4 \,dr - \frac{eQ}{4\pi\varepsilon_0}\frac{8}{21} \left(\frac{1}{a^5}-\frac{4}{b^5}
\right)
\int R_d(r)^2 r^6 \,dr
\\
\Delta E_{3d_{x^2-y^2}} = -\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right) -\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\left(\frac{1}{a^3}+\frac{1}{b^3}
\right) \int R_d(r)^2 r^4 \,dr -\frac{eQ}{4\pi\varepsilon_0}\frac{19}{42} \left(\frac{1}{a^5}+\frac{1}{b^5}
\right)
\int R_d(r)^2 r^6 \,dr
\end{gathered}
Переобозначим некоторые величины и перепишем
\begin{gathered}
C=-\frac{2Qe}{4\pi\varepsilon_0}\left( \frac{1}{a}+\frac{1}{b} \right)\\
A= -\frac{eQ}{4\pi\varepsilon_0}
\frac{2}{7}\int R_d(r)^2 r^4 \,dr \\
B= -\frac{eQ}{4\pi\varepsilon_0}\frac{1}{42} \int R_d(r)^2 r^6 \,dr
\\
\Delta E_{3d_{z^2}} = C - A \left(\frac{1}{a^3}+\frac{1}{b^3}\right) + 90B \left(\frac{1}{a^5}+\frac{1}{b^5}\right)
\\
\Delta E_{3d_{xy}} = C + A\left(\frac{1}{a^3}+\frac{1}{b^3}\right) - 16B\left(\frac{1}{a^5}+\frac{1}{b^5}\right)
\\
\Delta E_{3d_{xz}} = C + A\left(\frac{1}{a^3}-\frac{2}{b^3}\right) - 16B\left(\frac{4}{a^5}-\frac{1}{b^5}\right)
\\
\Delta E_{3d_{yz}} = C - A\left(\frac{2}{a^3}-\frac{1}{b^3}\right) + 16B\left(\frac{1}{a^5}-\frac{4}{b^5}\right)
\\
\Delta E_{3d_{x^2-y^2}} = C + A\left(\frac{1}{a^3}+\frac{1}{b^3}\right) + 19B\left(\frac{1}{a^5}+\frac{1}{b^5}\right)
\end{gathered}
Найдем разницу между соседними уровнями
\begin{gathered}
\Delta E_{3d_{x^2-y^2}}-\Delta E_{3d_{xy}}= 35B \frac{1}{a^5} +35B\frac{1}{b^5} \\
\Delta E_{3d_{xy}}-\Delta E_{3d_{z^2}} = 2A \frac{1}{a^3} + 2A\frac{1}{b^3}
-106B \frac{1}{a^5} -106B\frac{1}{b^5} \\
\Delta E_{3d_{z^2}}-\Delta E_{3d_{yz}} = A \frac{1}{a^3} - 2A\frac{1}{b^3} +
64B \frac{1}{a^5} +154B\frac{1}{b^5} \\
\Delta E_{3d_{yz}}-\Delta E_{3d_{xz}} = -3A \frac{1}{a^3} + 3A\frac{1}{b^3}
+80B\frac{1}{a^5} -80B\frac{1}{b^5} \\
\end{gathered}
Мы видим, что уровни реально разные, но возникает вопрос можно ли их сделать равноудаленными друг от друга. Если \Delta E одинаковые, то возникнет противоречие. Если хочется чтобы уровни были равноудаленными, придется делать не ромб, а еще нарушать дальше симметрию.
Подведем итог
Если b/a=k, то
\begin{gathered}
\Delta E_{3d_{z^2}} = C - \frac{A}{a^3} \left(1+k^3\right) + 90\frac{B}{a^5} \left(1+k^5\right)
\\
\Delta E_{3d_{xy}} = C + \frac{A}{a^3} \left(1+k^3\right) - 16\frac{B}{a^5} \left(1+k^5\right)
\\
\Delta E_{3d_{xz}} = C + \frac{A}{a^3} \left(1-2k^3\right) -16\frac{B}{a^5} \left(4-k^5\right)
\\
\Delta E_{3d_{yz}} = C - \frac{A}{a^3} \left(2-k^3\right) +16\frac{B}{a^5} \left(1-4k^5\right)
\\
\Delta E_{3d_{x^2-y^2}} = C + \frac{A}{a^3} \left(1+k^3\right) + 19\frac{B}{a^5} \left(1+k^5\right)
\end{gathered}
В случае квадрата k=1
\begin{gathered}
\Delta E_{3d_{z^2}} = C - 2\frac{A}{a^3} + 180\frac{B}{a^5}
\\
\Delta E_{3d_{xy}} = C + 2\frac{A}{a^3} - 32\frac{B}{a^5}
\\
\Delta E_{3d_{xz}} = C - \frac{A}{a^3} - 48\frac{B}{a^5}
\\
\Delta E_{3d_{yz}} = C - \frac{A}{a^3} -48\frac{B}{a^5}
\\
\Delta E_{3d_{x^2-y^2}} = C + 2\frac{A}{a^3} + 38\frac{B}{a^5}
\end{gathered}
Как и ожидалось 3d_{xz} и 3d_{yz} вырождены.
29 лайков
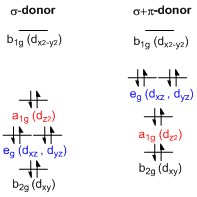
Вот это кстати веселый пример (с плоским квадратом). Если применять теорию лигандного поля, орбитали d_{xy}, d_{xz}, d_{yz} несвязывающие (в случае если у нас лиганты только \sigma доноры). Т.е. геометрия плоский квадрат должна быть 3:1:1. Я вот пытаюсь понять почему теория возмущений дает другой результат?
3 лайка
Вот к слову. Распределение МО для плоского квадрата там неверное. Ну может быть оно верно в рамках ТКП, но ТКП это дешевая, если не псевдонаучная теория.
Если строить МО, т.е. использовать ligand field theory, распределение будет другим. На странице в вики оно корректное:
Я так и не понял почему эту картинку с ТКП используют во всех учебниках если она откровенна неправильная. Я спрашивал своего профа, он говорит “ну хз, ТКП, че могу сказать”.
2 лайка
Прям так и сказал? XD
Ну типа. Он не особо знаком был с crystal field theory, LFT makes sense from first principles. CFT не очень. Разбираться почему именно она настолько ошибочна ни времени, ни желания не было.
Наверное потому что все сначала начинают с ТКП?[1] Чтобы читатель не растерялся увидив, что у него получается одна диаграмма, а в книге показана другая.
А это, наверное, потому, что ТКП проще. ↩︎
2 лайка
ТКП учитывает только электромагнитные взаимодействия. ТПЛ наоборот только ковалентные взаимодействия учитывает, забывая про энергию поля. В итоге в крайних случаях обе могут врать.
2 лайка
ты имеешь в виду, что по хорошему в гамильтониане нужен -q/c \mathbf{A}?