Используем Avogadro для визуализации геометрии молекул

[Anton (Anton Morgunov)]

Введение

При изучении химии нередко возникают ситуации, в которых необходимо хорошо представлять как выглядит молекула в трехмерном пространстве. Например, если мы хотим показать метилциклогексан в аксиальной конформации, мы его нарисуем так:

Но из такого изображения далеко не всегда понятно в чем собственно проблема аксиальной конформации, или, иными словами, откуда берется то самое 1,3-аксиальное стерическое отталкивание?

Другой пример: бициклобутан. Скелетная структура выглядит очень странно и можно задаться вопросом: а как такая (центральная) связь вообще может существовать? Ведь эта связь должна быть в 1.4 раза длиннее обычных С-С связей!

Для разрешения таких вопросов и более наглядного изучения химии можно пользоваться программой Avogadro.

Что такое Avogadro?

Прежде чем мы начнем использовать эту программу, стоит понять для чего она была создана: это программа для молекулярного моделирования, написанная в основном для использования в научных исследованиях. Например, для визуализации данных, полученных в результате квантовохимических вычислений^[1].

Иными словами, программа написана для исследователей, не для школьников, не для учителей, а значит она не обязана быть понятной и абсолютно интуитивной. Более того, наверное 80% функционала просто-напросто недоступны без результатов квантхим вычислений. И тем не менее, за оставшимися 20% этой программой стоит пользоваться в образовательных целях.

Установка Avogadro

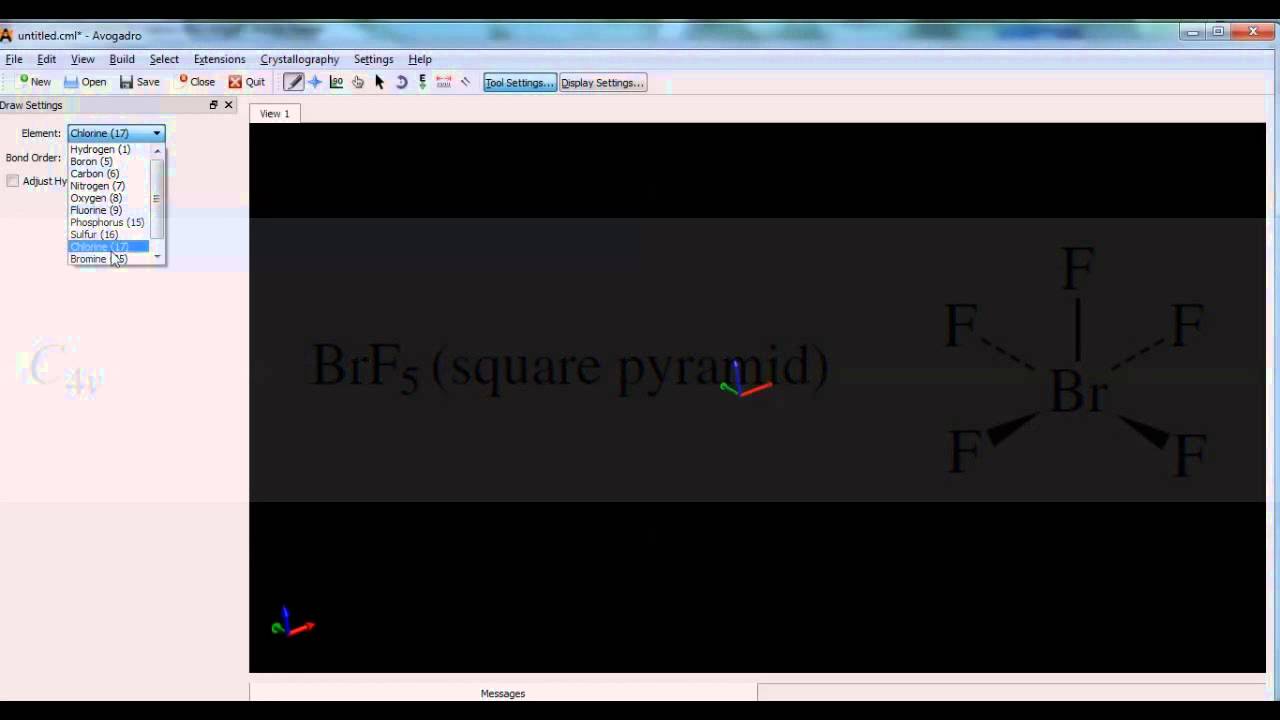
Заходим на сайт программы и жмем Download.. Должна скачаться версия 1.2.0.^[2] Еще один нюанс: эта версия была выпущена в 2016 году, а значит, неизбежно, ряд вещей может уже не работать.^[3]

Скачиваем, устанавливаем, радуемся.

Для чего можно использовать Avogadro?

Строим модели молекул

Поскольку лучше один раз увидеть, чем сто раз услышать, просто посмотрите видео:

Avogadro v1.1 Basics Of Modeling & Optimization

Находим оптимальную геометрию конформаций

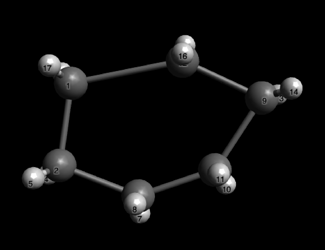
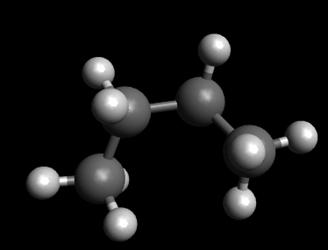
Вот скажем вы нарисовали циклогексан, но получился он не очень симметричным:

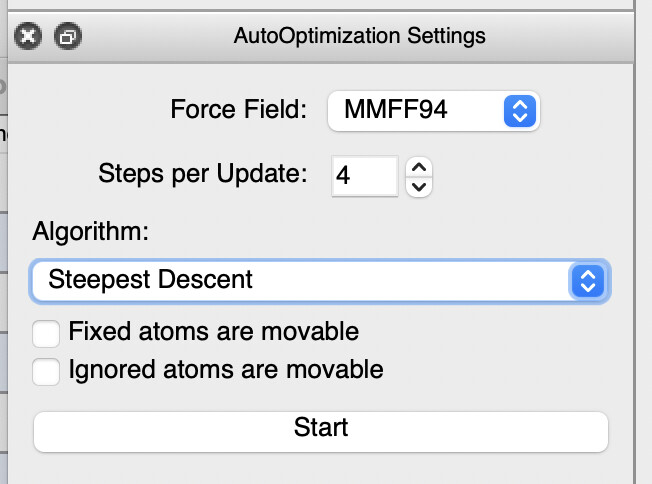
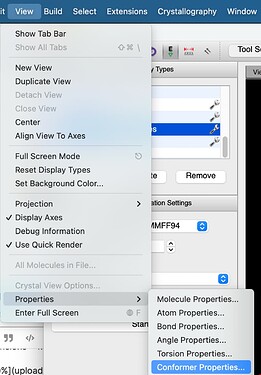
Жмем на иконку с буквой Е (auto optimization tool), выбираем Force field: MMF94 и жмем Start

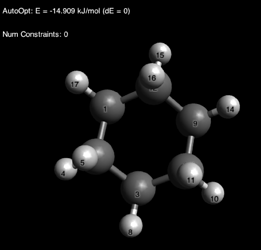
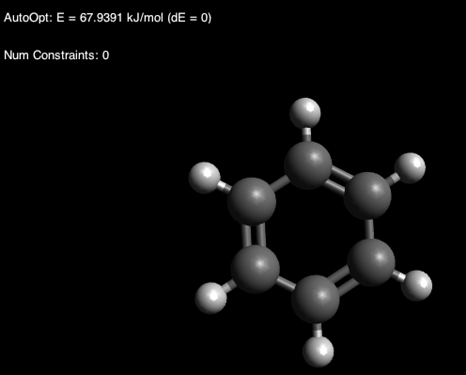
Через некоторое время вы можете наслаждаться прекрасной конформацией кресла:

У вас сразу может возникнуть вопрос: о, а там показывают энергию, что это значит? Ровным счетом ничего.^[4] Обращайте внимание только на полученную геометрию.

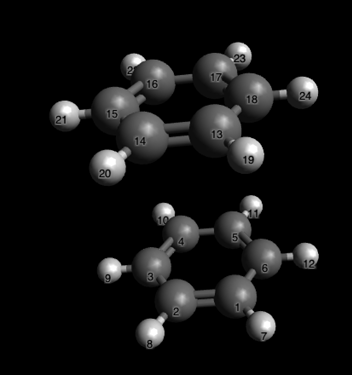
Давайте попробуем добавить метильную группу в аксиальное положение и заново оптимизируем структуру:

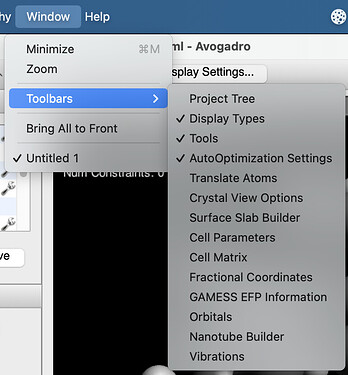
И теперь у нас почти все готово для того чтобы понять природу 1,3-стерического отталкивания. Осталось только открыть окошо Display Types:

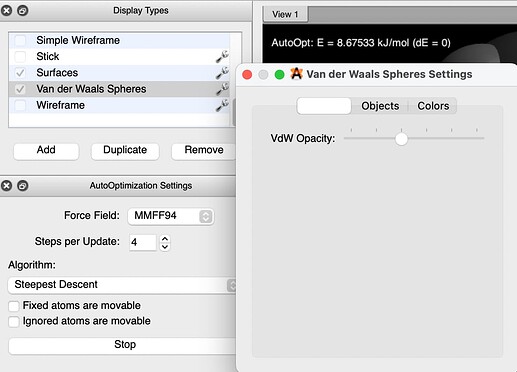
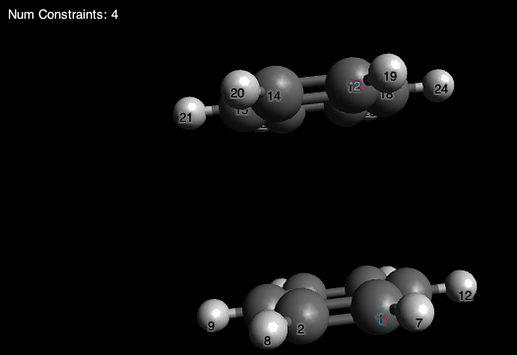
И поставить галочку возле Van der Waals Spheres (нажав на гаечный ключ можно регулировать прозрачность сфер):

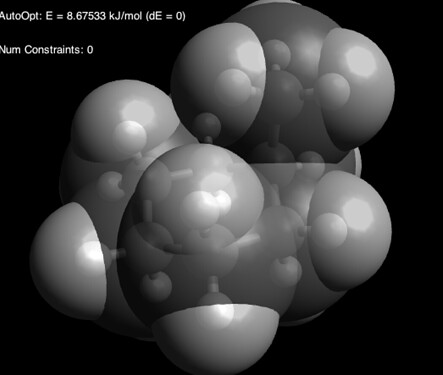
Тада! Мы видим, что атомы водорода метильной группы и аксиальные атомы водорода гораздо ближе друг к другу, чем кажется:

Дальнейшие шаги

В целом, в 99% случаев Авогадро пригодится вам именно как программа для поиска стабильной геометрии и визуализации молекул. Как вы могли догадаться, есть 1% не показанных выше возможностей. С ними можно ознакомиться в дополнительных сообщениях к этой теме:

• Поиск конформаций
• Изучение химических сэндвичей

В отдельном сообщении рассказано о том что такое силовые поля и как авогадро находит оптимальные геометрии.

---

1. Пионером квантхим вычислений была программа Gaussian, но сопровождающий софт для визуализации GaussView продается за отдельную плату ($750 за одну лицензию для академического использования). Понятное дело, что платить такие деньги крайне неприятно и в таких условиях рождаются открытые open source проекты как Avogadro. ↩︎

2. Вы можете наткнуться на т.н. Avogadro2, которая находится в бета версии и имеет нумерацию 1.97. Если коротко – по состоянию на август 2022 г. эту версию можно смело игнорировать. Это сплошное разочарование, никаких положительных эмоций она у меня не вызывает. ↩︎

3. Например на macOS еще со времен Catalina перестала работать визуализация МО, но для вас это не проблема – для МО нужны квантхим расчеты. ↩︎

4. Абсолютные значения этой энергии абсолютно бессмысленны. В очень редких случаях ими можно пользоваться в сравнительном ключе. ↩︎

[Anton (Anton Morgunov)]

Поиск конформеров

В очень редких случаях, Avogadro может искать конформации молекул. Проверенно работает для двух молекул: бутана и этилциклогексана. Давайте построим бутан и оптимизируем его структуру (MMF94). Не забываем нажать Stop в Optimization Tool.

Дальше идем в Extensions > Molecular Mechanics > Conformer Search…

И убеждаемся, что number of rotatable bonds равно 1 (очень часто оно равно нулю, даже если такие связи есть. В таком случае Авогадро просто не может искать конформеры). Выставляем параметры как на скрине и жмем ОК.

По завершению идем в View > Properties > Conformer Properties

И отсортировав значения по энергии видим, что Авогадро находит два конформера:

Нажимая на значения энергии конформеров мы получаем структуры, которые им соответствуют. А еще это тот самый редкий случай, когда значение энергии имеет небольшой смысл: мы узнаем какая конформация стабильнее.

[Anton (Anton Morgunov)]

Изучение химических сэндвичей

Авогадро можно использовать для рассмотрения \pi-\pi взаимодействий.

Для начала возьмем экспериментальную геометрию бензола. Если вы сохраните следующие данные в файле c расширением .xyz^[1], например benzene.xyz, вы можете открыть этот xyz файл в Авогадро и увидеть привычную гаечку.

12
Experimental geometry for benzene
C	0.0000	1.3970	0.0000
C	1.2098	0.6985	0.0000
C	1.2098	-0.6985	0.0000
C	0.0000	-1.3970	0.0000
C	-1.2098	-0.6985	0.0000
C	-1.2098	0.6985	0.0000
H	0.0000	2.4810	0.0000
H	2.1486	1.2405	0.0000
H	2.1486	-1.2405	0.0000
H	0.0000	-2.4810	0.0000
H	-2.1486	-1.2405	0.0000
H	-2.1486	1.2405	0.0000

Если открыть этот файл в Авогадро и запустить оптимизацию структуры в MMF94, геометрия не изменится, но мы можем зафиксировать значение энергии: \pu{E= 67.9391 kJ mol-1}.

Теперь сделаем наш сэндвич: расположим еще одну молекулу бензола прям над первой на расстоянии 4.5 \AA.

24
Experimental geometry for benzene
C	0.0000	1.3970	0.0000
C	1.2098	0.6985	0.0000
C	1.2098	-0.6985	0.0000
C	0.0000	-1.3970	0.0000
C	-1.2098	-0.6985	0.0000
C	-1.2098	0.6985	0.0000
H	0.0000	2.4810	0.0000
H	2.1486	1.2405	0.0000
H	2.1486	-1.2405	0.0000
H	0.0000	-2.4810	0.0000
H	-2.1486	-1.2405	0.0000
H	-2.1486	1.2405	0.0000
C	0.0000	1.3970	4.5000
C	1.2098	0.6985	4.5000
C	1.2098	-0.6985	4.5000
C	0.0000	-1.3970	4.5000
C	-1.2098	-0.6985	4.5000
C	-1.2098	0.6985	4.5000
H	0.0000	2.4810	4.5000
H	2.1486	1.2405	4.5000
H	2.1486	-1.2405	4.5000
H	0.0000	-2.4810	4.5000
H	-2.1486	-1.2405	4.5000
H	-2.1486	1.2405	4.5000

Откроем в Авогадро. Сэндвич выглядит так (я включил отображение Labels в Display Types)

Давайте замерим расстояние между атомом углерода 1 и 13. Для этого выберем инструмент линейки и нажмем на эти два атома по очереди:

Расстояние 4.5 \AA, как мы и хотели:

Прежде чем запустим оптимизацию структуры, надо установить некоторые ограничения, чтобы одна молекула бензола оставалась параллельна второй. Для этого идем в Extensions → Molecular Mechanics → Constraints…

И выставляем Fix atom X и Fix atom Y по очереди для атомов 1 и 13 (т.е. мы фиксируем их x и y координаты, они не могут меняться при оптимизации):

Жмем ОК и запускаем оптимизацию с MMF94. Если вы все сделали правильно, вы увидите Constraints: 4 и через минуту (или две) оптимизация завершится:

И тут у нас снова тот редкий случай, когда мы можем хоть что-то сделать с показателями энергии. Посмотрите на значение энергии, который получился в результате оптимизации сэндвича. Отнимите от этого значения две энергии бензола (\pu{E= 67.9391 kJ mol-1}, как было найдено выше) и вы получите энергию \pi-\pi взаимодействия.

Более точными квантовохимическими расчетами^[2] можно получить расстояние между молекулами бензола в 3.9 \AA и энергию взаимодействия в районе \pu{7.32 kJ mol-1}. Насколько результаты MMF94 близки к этим числам? Повторите расчеты с силовым полем GAFF.

---

1. xyz файлы имеют следующую структуру: на первой строчке указано количество атомов (N) в молекуле, вторая строчка для комментариев, а последующие N строчек указывают вид атома и его расположение в трехмерном пространстве: координаты (x,y,z) в \AA. 1\AA = \pu{10^-10 m} ↩︎

2. CCSD(T) в complete basis set limit ↩︎

[Anton (Anton Morgunov)]

Теория силовых полей

Введение

Некоторые из вас могут знать, что для точного описания молекул в современном мире пользуются инструментами квантовой механики. А именно, мы находим приблизительные^[1] решения уравнения Шредингера: \hat{H}\psi=E\psi. Только значения энергии, полученные в результате решения этого уравнения, имеют хоть какой-то смысл. Но для решения уравнения Шредингера надо пользоваться специальными программами. Авогадро, сам по себе, решать уравнение Шредингера не может. Так каким же образом Авогадро может из вот такого:

за 15 секунд (!!!) получить такое:

Для сравнения: полноценная оптимизация с помощью квантхим расчетов занимает 9 минут на 16 ядрах. Более разумное использование вычислительной мощности предполагает предварительную оптимизацию с помощью силовых полей (именно для этого и нужна программа Avogadro), а потом уже запускается квантхим расчет, который уже вносит более мелкие правки.

квантхим структура циклогексана

Вы можете сравнить структуру циклогексана полученную оптимизацией с помощью силовых полей с результатом квантхим расчета, запущенного на структуру, полученную после оптимизации силовыми полями:

18
m062x/6-311++g**
  C   -6.15715325909063      2.80912162906656     -0.46413309054229
  C   -5.91060040366610      1.37875874420885      0.02390587846359
  C   -4.51246463282831      0.89510750688241     -0.36947651892596
  H   -6.67239340625346      0.70398898216743     -0.37597814748720
  H   -6.00418885000189      1.35191693519906      1.11668641186672
  C   -3.43333039443439      1.84918855476994      0.14933028303980
  H   -4.44687852535120      0.84007331476681     -1.46315068592265
  H   -4.34010597573618     -0.11595496364762      0.00982325793993
  C   -3.67988270651451      3.27955101683420     -0.33870992386706
  H   -2.44261989594814      1.50680519916000     -0.16170476309751
  H   -3.44345830169053      1.83845171850945      1.24636703039508
  C   -5.07801842693904      3.76320259650785      0.05467286691146
  H   -3.58629480275193      3.30639169599838     -1.43149048510481
  H   -2.91808991745623      3.95432118337116      0.06117378539438
  H   -5.25037685038842      4.77426511738709     -0.32462681411686
  H   -5.14360350680610      3.81823682944012      1.14834709926776
  H   -7.14786325414253      3.15150494646967     -0.15309635161242
  H   -6.14702689000040      2.81985899290864     -1.56116983260197

Базовые обозначения

В самом начале есть пара не очень интуитивных допущений (которые рассматриваются детальнее в квантовой механике):

Возьмем молекулу. Определенному расположению (\vec{R}, это 3N-мерный вектор, где N – количество атомов в молекуле) ядер всех атомов в молекуле соответствует определенное распределение электронной плотности^[2]. Почему мы можем “разделять” положение ядер и электронов? Потому что электрон в 1836 раз легче протона. В рамках определенных приближений, мы говорим, что электроны двигаются настолько быстро, что достигают своего равновесного расположения быстрее, чем какое-то ядро успеет подвинуться.

А теперь ключевой момент: как мы сказали, определенному положению ядер \vec{R} соответствует определенная электронная плотность, с соответствующей энергией V(\vec{R}). Если мы будем варьировать \vec{R}, то мы будем получать разные значения V(\vec{R}). По сути, мы получаем кривую потенциальной энергии для движения ядер в поле электронов. Мы можем получить точное выражение для V(\vec{R}) из квантовой механики. А можем попробовать найти классическое приближение. Этим и займемся.

Чуть больше деталей для любителей математики.

Если есть скалярное поле потенциальной энергии V(\vec{R}), мы можем посчитать силу, которая действует на определенный атом i, находящийся в положении (x_i,y_i,z_i): \vec{F_i}= \nabla_i V , где

\nabla_i = \hat{i} \cdot \frac{\partial}{\partial x_i} + \hat{j} \cdot \frac{\partial}{\partial y_i} + \hat{k} \cdot \frac{\partial}{\partial z_i}

Поскольку одним движением мы получаем силу, действующую на любой из атомов, мы и называем поле V(\vec{R}) силовым полем (force field)^[3]

Какие взаимодействия есть в молекулах?

Давайте попробуем построить выражение для потенциальной энергии V(\vec{R}) исходя из соображений классической механики.

Химические связи

Давайте смоделируем химическую связь как гармонический осциллятор. Для любой связи между атомами X и Y (вне зависимости от того, с какими другими атомами они связаны^[4]) существует определенная характерная длина связи r_0 и определенная характерная жесткость, пропорциональная силе связи, которую мы обозначим как k_{XY}. Тогда потенциальная энергия связанная с изменением длины связи X-Y имеет простую форму:

V_{bond}=\frac{1}{2}k_{XY}(r-r_0)^2

Например, для типичной связи C-C: r_0=1.523 \AA и k_{XY}=\pu{317 kcal mol-1 \mathring{A}-2}.

Углы химических связей

Представим фрагмент A-B-C. Предыдущее выражение позволяет определить расстояния A-B и B-C. А что насчет угла \angle ABC? Давайте тоже его смоделируем потенциалом, похожим на гармонический осциллятор! Для любого угла XYZ есть характерное значение \alpha_0 и k_{XYZ}. Тогда потенциальная энергия для отклонений от \alpha_0 будет равна:

V_{angle} = \frac{1}{2} k_{XYZ} (\alpha-\alpha_0)^2

Например, для типичной С-С-С связи: \alpha_0=109.47\degree и k_{XYZ}=\pu{0.0099 kcal mol-1 \mathring{A}-2}. Обратите внимание, что значение константы на 5 порядков ниже, чем для растяжения связей!

Ван-дер-Ваальсовы взаимодействия

Два атома X и Y, не образующие связь X-Y (как, например, аксиальные водороды) и даже не участвующие ни в одной последовательности связей X-A-Y (как в случае сэндвича) по прежнему могут взамодействовать с помощью дисперсионных сил. C другой стороны, если атомы X и Y приблизятся слишком близко (ближе, чем сумма их радиусов Ван-дер-Ваальса)^[5], между ними должно быть отталкивание. Одним из способов смоделировать отталкивание на близких расстояниях и притягивания на дальних является потенциал Леннарда-Джонса:

V_{LJ} = \epsilon \left[ \left(\frac{r_e}{r} \right)^{12}- 2\left(\frac{r_e}{r} \right)^{6} \right]

Где -\epsilon максимальное стабилизационное взаимодействие, наблюдаемое при r=r_e. Такой потенциал называют LJ 12-6 (в соответствии с показателями степеней). Иногда могут использоваться и другие LJ m-n потенциалы.

Кулоновское отталкивание

Как мы могли забыть, что атомы это заряженные частицы, несущие заряд q_X и q_Y? Между ними есть кулоновское отталкивание:

V_{electrostatic}=\frac{q_X q_Y}{r}

Торсионное взаимодействие

Давайте добавим еще слагаемое, которое учитывает изменение энергии при вращении связи Y-Z в последовательности W-X-Y-Z^[6]:

V_{tors}=A_{X-Y-Z-W}(1-\cos n\omega)

где \omega – торсионный угол, а n – количество барьеров при одном полном вращении. Например, для этана n=3.

Смешанные слагаемые

Для большей точности мы можем добавить т.н. coupling (mixed) terms, которые учитывают одновременно длину связи и угол. Пример: очевидно, что угол X-Y-Z должен зависеть от длины связей X-Y и Y-Z. Мы можем учитывать такие зависимости с дополнительными слагаемыми.

Что у нас в итоге:

Просуммируем по всем связям, всем углам, всем дисперсионным взаимодействиям и т.п.:

V = \sum_{X-Y} \frac{1}{2} k_{XY} (r-r_0)^2+ \sum_{X-Y-Z} \frac{1}{2} k_{XYZ} (\alpha-\alpha_0)^2 + \sum_{X\dots Y} V_{LJ} +

+ \sum_{X,Y} \frac{q_X q_Y}{r} + \sum_{tors} A_{XYZW}(1-\cos n\omega) + \dots

Давайте определим характерные значения констант для всех атомов^[7] и мы получим наше силовое поле!

Некоторые силовые поля

GAFF (Amber) Class I

Уравнение, которое мы записали выше, ложится в основу силового поля GAFF, доступного в Авогадро! Это силовое поле первого поколения.

Еще раз – мы получаем неплохие приближения структур молекул только с помощью классической механики!

UFF Class I+

В UFF добавлен ряд небольших уточнений.

MMF94 (MMF94s) Class II

В этом силовом поле добавляются:

• слагаемые 4 степени для описания длины хим связей, условно: (r-r_0)^4
• слагаемые 3 степени для описания углов хим. связей
• кросс-слагаемые связывающие длины связей с углами
• заряд атомов корректируется с учетом того, с какими другими атомами они связаны.

---

1. Точные решения существуют только для систем с 1 электроном. ↩︎

2. которое находится решением уравнения Шредингера ↩︎

3. Что, конечно, может резать ухо физикам, ибо они определяют силовое поле как векторное поле \vec{F}(\vec{R}) ↩︎

4. Что, конечно же, сильное упрощение. Но оно позволяет нам использовать одно выражение V(\vec{R}) для любых молекул. ↩︎

5. Именно радиусы Ван-дер-Ваальса показываются если нажать на опцию Van-der-Waals spheres. ↩︎

6. Внимательный читатель возразит: а разве мы не учитываем эти изменения как Ван-дер-Ваальсовы силы? Ответ: учитываем, но на практике нужно добавить еще одно слагаемое, чтобы получать результаты, которые ближе к экспериментальным данным. ↩︎

7. Например, с помощью квантовохимических расчетов. ↩︎