Гидростатика давление

Физика Механика
1

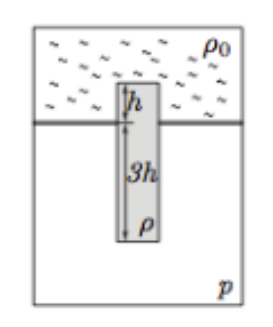
image

В герметичном сосуде сверху находится жидкость с плотностью ρ0 = 800 кг/м3
, отделённая
легким подвижным поршнем от газа (см. рисунок), находящегося внизу и имеющего давление p =
20 кПа. В поршне есть круглое отверстие, в которое вставлен цилиндрический поплавок, причём в
жидкость поплавок погружён на некоторую длину h, а в газ — на длину 3h. Площадь основания
поплавка S. Поплавок может свободно скользить относительно поршня, а поршень — относительно
стенок сосуда. Жидкость нигде не подтекает. Какой должна быть плотность поплавка ρ, чтобы
система могла оставаться в равновесии?

2

смотри давай для начала представим что верхняя часть сосуда имеет высоту H

  • теперь в верхней точке поплавка создается давление p0= \rho (H-h) g
  • теперь из состоянии равновесия имеем следующее уравнение = p0S + mg=pS
  • теперь рассмотрим поршень он ведь тоже не двигается: а это значит что сверху давления от (веса) жидкости, то есть наш p0 уравновешан P ==> \rho H g S2= pS2
    далее единственным уравнением остается m=\rho 4h g
    и все решится
4 лайка
3

Вам помог ответ? Есть какие-то дополнительные вопросы?