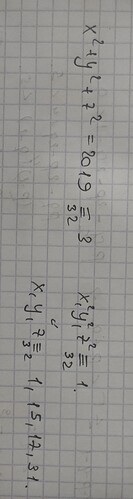x^2+y^2+z^2=2019
x, y, z - натуральные числа.
Пытался рассуждать так: 2019 делится на три, но не делится на девять. Значит, данные три числа не делятся на три (иначе сумма квадратов делилась бы на девять). 2019 = 3 по модулю 4. Отсюда выходит, что все три числа нечетны. Значит, придется перебрать все тройки нечетных, не делящихся на три чисел от 1 до 44. Если честно, решение кажется корявым. Как можно его улучшить?
чтобы облегчить вам жизнь: пусть х≥у≥z, тогда x≥26
ваши рассуждения верны, но решение не закончено. попробуйте рассмотреть последние цифры квадратов, тогда число возможных вариантов х сузится до 6
если не поняли мысль
последние цифры квадратов: 0, 1, 4, 5, 6, 9
мы установили, что х,у,z нечётны. следовательно, из вариантов остаются: 1, 5, 9
сумма тройки чисел, оканчивающихся этими цифрами, будет оканчиваться на 1, 3, 5, 7, 9
учитывая, что 26≤х≤44, и то, что х окнчивается на одну из вышеперечисленных цифр — х может быть равен только 29, 31, 35, 37, 41, 43
дальше легко) рассматриваете 6 случаев y²+z² (не забывайте про наши ограничения) и получаете 9 троек чисел.
2 лайка