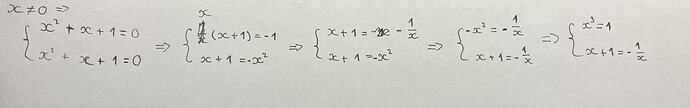задача:
x^2+x+1=0
домножим на 1/x
x+1+1/x=0
из первого: x+1=-x^2
подставим под второе
1/x+(-x^2)=0
1/x=x^2
x^3=1
то есть x=1
вопрос: откуда лишний корень если он не подходит под изначальное уравнение
1 лайк
Как я понял, из задачи можно понять, что уравнение не имеет действительных корней, потому что
D=b^2-4ac=-3<0
Таким образом, уравнение имеет два комплексных корня
x_(1,2)=\frac{-b\pm\sqrt D}{2a}
x_(1,2)=\frac{-1\pm\sqrt -3}{2}=\frac{-1\pm i\sqrt3}{2}
2 лайка
Если у нас есть многочлен P(x), при решении уравнения P(x) = 0, мы ищем нули функции f(x) = P(x). В данном случае:
f(x) = x^2 + x + 1,\\
f(x) = 0.
Если обе стороны уравнения помножить на \displaystyle \frac{1}{x}, мы уже получим другую функцию
g(x) = x + 1 + \frac 1x,
и уравнение g(x) = 0.
Технически, здесь ты говоришь, что собираешься решать систему уравнений
\begin{cases}
f(x) = 0,\\
g(x) = 0.
\end{cases}
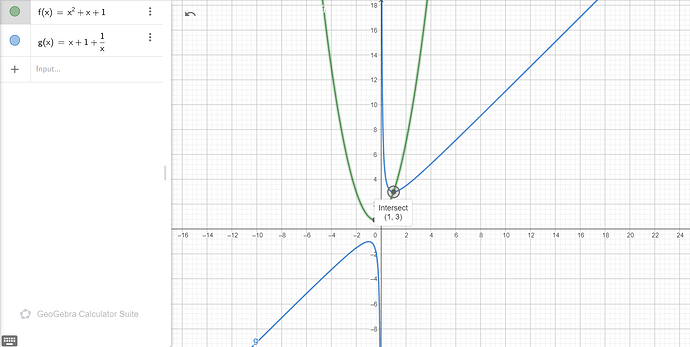
x = 1 является решением данной системы. Более наглядно это можно понять изобразив это графически:
P.S. В будущем рекомендую очень консервативно использовать домножение на неизвестную перемененную и тем более деление на неё, потому что одно из решений может оказаться нулевым. В таких случаях решение не засчитывается правильным.
P.P.S Меня бы моя учительница математики на месте убила за такой финт как домножение на переменную
9 лайков
Не является же, по твоей картинке x = 1 это решение f(x) - g(x) = 0, а не системы
Тут ты должен сказать что допускаешь что x \neq 0
То есть формально:
x \neq 0 \implies x + 1/x + 1 = 0
Дальше
Что позволяет тебе подставлять в уравнения? Ты предполагаешь что x тут и там один и тот же. Ты решаешь систему уравнений.
Ну и вот ты решал систему уравнений, x^3 = 1 имеет три корня, но из них ты должен взять только те корни которые являются корнями остальных уравнений в системе. На картинке снизу написано то что ты пытался делать:
3 лайка