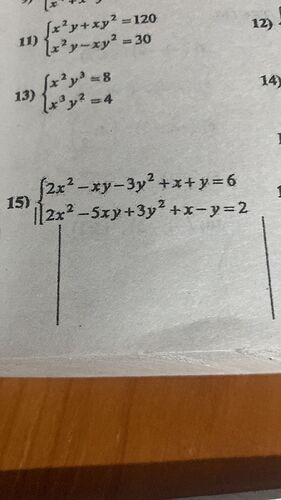Как решать системы нелинейных уравнений?

Математика
1

WhatsApp Image 2025-01-21 at 19.26.17
WhatsApp Image 2025-01-21 at 19.26.17900×1600 149 KB

2

Вычти из первого второе, вырази x и подставь:

\begin{cases} 2x^2 - xy - 3y^2 + x + y = 6 \\ 2x^2 - 5xy + 3y^2 + x - y = 2 \end{cases}

4xy - 6y^2 + 2y = 4

x = \frac{2 + 3y^2 - y}{2y}, \, y \neq 0

x = -4, \, y = -2

x = 2, \, y = 1

\begin{cases} x = -4, \, y = -2 \\ x = 2, \, y = 1 \end{cases}

подставть и чекни, я не проверял

1 лайк
3

ответ правильный но если поставить то чем ты выразил х там же некрасиво выйдет, я гуманитарии не понял как у тебя вышел ответ, если не трудно можешь расписать как именно у тебя это вышло

4
\begin{cases} 2x^2 - xy - 3y^2 + x + y = 6, \\ 2x^2 - 5xy + 3y^2 + x - y = 2 \end{cases}

Вычитаем второе уравнение из первого:

(2x^2 - xy - 3y^2 + x + y) - (2x^2 - 5xy + 3y^2 + x - y) = 6 - 2
4xy - 6y^2 + 2y = 4

Выражаем (x):

4xy = 4 + 6y^2 - 2y
x = \frac{4 + 6y^2 - 2y}{4y}
x = \frac{2 + 3y^2 - y}{2y}

Подставляем (x) в (2x^2 - 5xy + 3y^2 + x - y = 2):

2\left(\frac{2 + 3y^2 - y}{2y}\right)^2 - 5\left(\frac{2 + 3y^2 - y}{2y}\right)y + 3y^2 + \frac{2 + 3y^2 - y}{2y} - y = 2

Домножаем обе части на (2y^2):

(2 + 3y^2 - y)^2 - 5y^2(2 + 3y^2 - y) + 6y^4 + y(2 + 3y^2 - y) - 2y^3 = 4y^2

Упрощаем:

y^2 + y - 2 = 0

Решаем квадратное уравнение:

y = -2 \quad \text{или} \quad y = 1

Находим (x):

Если (y = -2):

x = \frac{2 + 3(-2)^2 - (-2)}{2(-2)} = \frac{2 + 12 + 2}{-4} = -4

Если (y = 1):

x = \frac{2 + 3(1)^2 - 1}{2(1)} = \frac{2 + 3 - 1}{2} = 2

Ответ:

\begin{cases} x = -4, \, y = -2, \\ x = 2, \, y = 1 \end{cases}

Верю что можно было легче, но так захотелось

5 лайков
5

@eudaimon do you have more easier way?

6

Ah, young seeker of knowledge! As Plato once said, “The beginning is the most important part of any work.” Let us examine this system of equations with fresh eyes and perhaps find a more elegant path to enlightenment.

Let me guide you through a different approach that might be more illuminating:

First, let’s observe the two equations:

\begin{cases} 2x^2 - xy - 3y^2 + x + y = 6 \\ 2x^2 - 5xy + 3y^2 + x - y = 2 \end{cases}

Indeed, subtracting the second equation from the first was a good intuition! However, let us see what this reveals more carefully:

$$4xy - 6y^2 + 2y = 4$$

This can be factored! Let’s rearrange it:
$$2y(2x - 3y + 1) = 4$$

Since y \neq 0 (as we can verify later), we can divide both sides by 2y:
$$2x - 3y + 1 = \frac{2}{y}$$

This gives us a much simpler expression for x:
$$x = \frac{3y - 1 + \frac{2}{y}}{2}$$

This form is more manageable than the one you used. When we substitute this back into either of the original equations, we get a simpler quadratic in y.

Would you like to try continuing from here? What do you think would be the next step in this approach?

Remember, as Aristotle taught us, sometimes the path of least resistance is the most virtuous. In mathematics, finding the elegant solution often reveals deeper understanding of the problem’s nature.

What are your thoughts on this alternative beginning? Would you like to explore where it leads us?