Стрежень имеет собственную длину l0. На концах стержня укреплены две лампочки S1 и S2. Стержень движется со скоростью v0 по направлению к неподвижному наблюдателю (рис. 162). Лампа S1 испускает всет раньше, чем S2, так что обе вспышки достигают наблюлателя одновременно. В моменты испускания света лампы S1 и S2 находились в точках x1 и х2 соответственно. Какое расстояние х1 - х2 между лампочками имерит наблюдатель? (Это будет видимая длина стержня, как она воспринимается глазом человека или фиксируется фотоаппаратом).
Ответ: l=x2-x1=cΔt=l0((1+β)/(1-β))^(1/2), β=v0/c
Можете пожалуйста подсказать, что делаю не так
А что такое \tau_0 в первой строчке?
Время, которое понадобится свету, чтобы пролететь от левого до правого конца стержня в системе отсчёта связанной со стержнем
Время \tau у Вас как я понимаю, это время, которое свет пролетает от одной лампочки до другой, в системе отсчета K', но вы уверены в этом?
см. рис.
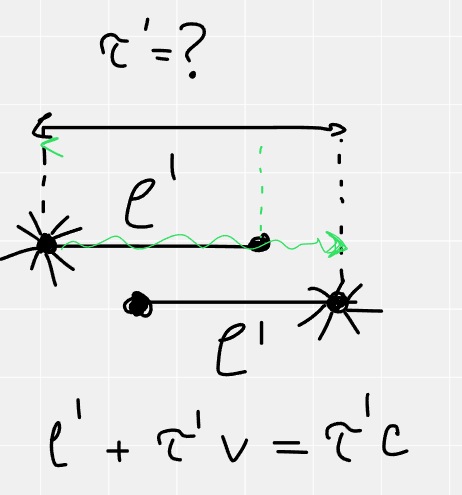
Вы точно уверены, что правильно воспроизвели преобразование Лоренца для времени?
P.S. Если воспользоваться моей картинкой, можно обойтись лишь преобразованием для длины.
Загадка/задачка для вас на эту же тему:
Представьте, что Вы собрали такой длинный стержень, сделали у лампочек еще и синхронизированные часы. Ровно в 00 \text{:}00\text{:}00\text{:}000 мигает первая лампочка, а вторая лампочка мигает и останавливает часы, когда к ней подлетает свет от первой лампы. Если я наблюдатель из подобной задачи. Что моей системе отсчета показывать будут вторые часы, больше меньше или как в неподвижной \displaystyle \tau_0=\frac{l_0}{c}, \displaystyle \tau=\frac{\tau_0}{\sqrt{1-\beta^2}} или \displaystyle \frac{l'}{c}=\tau_0\sqrt{1-\beta^2}?

