Please help in solving this problem.
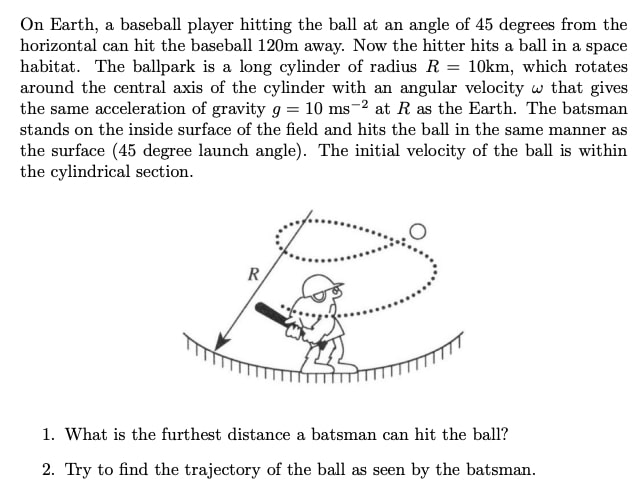
The “surface” in the 2nd last line above the figure implies Earth.
1 лайк
Interstellar 
2 лайка
Christopher Nolan created this problem…
2 лайка
Do give a difficulty rating for this problem as well
1 лайк
The first part can be solved in lab frame (where we see how the cylinder rotates), but it requires a bit of brute force (I ended up getting a negative answer lol, so I’m trying to solve it again).
2 лайка
I’ve got 3730 m, a length of the arc
2 лайка
Oh ok let me check
1 лайк
Ok so for the first part they have given two answers: 108m and 132m
1 лайк
For the second part we may solve the problem in accelerated frame of reference in cylindrical coordinates, with angular velocity \vec\omega =\omega\hat z (generally, \vec\omega =\pm\omega\hat z). So the ball was initially at
r =R,\quad \theta =0,
and \theta increases counter clockwise. At arbitrary moment the centripetal and Coriolis accelerations act on the ball:
\ddot{\vec r} = \omega^2\vec r - 2(\vec\omega\times\dot{\vec r}).
So we should differentiate the coordinates of the ball with respect to time (using \dot{\hat r} = \dot\theta\hat\theta, and \dot{\hat\theta}= -\dot\theta\hat r, in order to understand these relations, consider a small change of directions of \hat r and \hat \theta):
\vec r = r\hat r,\\\dot{\vec r} = \dot r\hat r+r\dot{\hat r} = \dot r\hat r +r\dot\theta\hat\theta,\\\ddot{\vec r}=\ddot r\hat r+2\dot r\dot\theta\hat\theta+r\ddot\theta\hat\theta-r\dot\theta^2\hat r.
Now, using \hat z\times\hat r=\hat\theta and \hat z\times\hat\theta=-\hat r, we can expand the Coriolis acceleration:
\ddot{\vec r} = \omega^2r\hat r - 2\omega(\dot r\hat\theta-r\dot\theta\hat r).
Now, dividing into components, we get the following equations:
\begin{cases}\ddot r -r\dot\theta^2 = \omega^2r+2\omega r\dot\theta,\\2\dot r\dot\theta+r\ddot\theta=-2\omega\dot r.\end{cases}
(I hope I didn’t make any silly mistakes there.) So basically we have to find a r(\theta) function with these equations and initial conditions.
Ok, I’ll find out where I was wrong.
3 лайка
Ohk, for the second part, they have got a complicated equation…
1 лайк
I think your second part approach is correct… I too was thinking along same lines but couldnt proceed far(i am dumb so thats not surprising)
1 лайк
Well, what I did next is rearranged the 2nd equation (using chain rule \displaystyle\ddot\theta=\frac{d\dot\theta}{dt}=\frac{d\dot\theta}{d\theta}\frac{d\theta}{dt}=\dot\theta\frac{d\dot\theta}{d\theta})
\ddot\theta=\dot\theta\frac{d\dot\theta}{d\theta}=-\frac{2\dot r}{r}(\omega+\dot\theta)\quad\Rightarrow\quad\frac{\dot r}{r}=-\frac{1}{2}\frac{\dot\theta d\dot\theta}{(\omega+\dot\theta)d\theta}=\frac{1}{r}\frac{dr}{dt}=\frac{\dot\theta}{r}\frac{dr}{d\theta},
so
\frac{dr}{r}=-\frac{1}{2}\frac{d\dot\theta}{\omega+\dot\theta}.
Integrating yields
r=\frac{C_1}{\sqrt{\omega+\dot\theta}}
As for the first equiation:
\frac{\ddot r}{r}=\frac{\dot\theta}{r}\frac{d\dot r}{d\theta}=\frac{\dot\theta}{r}\frac{d}{d\theta}\left(\dot\theta\frac{dr}{d\theta}\right)=\dot\theta^2+2\omega\dot\theta+\omega^2=(\omega+\dot\theta)^2.
So, obtaining \dot\theta from the second equation \displaystyle\left(\dot\theta=\omega+\frac{C_1^2}{r^2}\right) and plugging into the latter thing gives
\left(\frac{\omega}{r}+\frac{C_1^2}{r^3}\right)\cdot\frac{d}{d\theta}\left(\frac{dr}{d\theta}\left(\omega+\frac{C_1^2}{r^2}\right)\right)=\frac{C_1^4}{r^4}.
(lemme take a break, the thing has become too difficult)
5 лайков
\frac{\ddot r}{r}=\frac{\dot r}{r}\frac{d\dot r}{dr} = \frac{d(\dot r^2)}{d(r^2)},\quad (\omega+\dot\theta)^2 = \frac{C_1^4}{r^4}\quad\Rightarrow\quad d(\dot r^2)=\frac{C_1^4}{r^4}d(r^2),
\dot r^2 = \left(\dot\theta\frac{dr}{d\theta}\right)^2=-\frac{C_1^4}{r^2}+C_2,
d\theta = \frac{\displaystyle\omega+\frac{C_1^2}{r^2}}{\displaystyle C_2-\frac{C_1^4}{r^2}}\cdot dr
You know, maybe this problem needs a different approach (maybe solving it in Cartesian coordinates?)
3 лайка
Yeah bro take a break and it is fine… Let me just say that I am extemely grateful to you for taking soo much time and effort to help me… Not many people are like you. 
You have already cleared a lot of stuff from this problem… thank you again:pray:
5 лайков
Yeah, I think this is a bit too much on the difficult side. I’ll try asking some people in the nearby institute center.
2 лайка
I found out that I put a redundant negative sign while writing accelerations, so after correcting my solution I found out that the latter expression can be (not) easily integrated.
\int d\theta = \int\frac{C_1^2+\omega r^2}{C_2r^2-C_1^4} \cdot dr=\int\left(\frac{C_1^2}{C_2r^2-C_1^4}+\frac{\omega}{C_2}\frac{C_2 r^2}{C_2r^2-C_1^4}\right)\cdot dr=
=\int\left(\frac{C_1^2}{C_2r^2-C_1^4}+\frac{\omega}{C_2}\left(1+\frac{C_1^4}{C_2r^2-C_1^4}\right)\right)\cdot dr =
=\int\left(\frac{\displaystyle C_1^2+\frac{\omega C_1^4}{C_2}}{C_2r^2-C_1^4}+\frac{\omega}{C_2}\right)\cdot dr =
= \left( C_1^2+\frac{\omega C_1^4}{C_2}\right)\int\frac{dr}{C_2r^2-C_1^4} + \frac{\omega}{C_2}\int dr =
=\left( C_1^2+\frac{\omega C_1^4}{C_2}\right)\int\left(\frac{1/2C_1^2}{\sqrt C_2 r -C_1^2}-\frac{1/2C_1^2}{\sqrt C_2r+C_1^2}\right)dr + \frac{\omega r}{C_2} =
=\left(\frac{1}{2}+\frac{\omega C_1^2}{2C_2}\right)\cdot\frac{1}{\sqrt C_2}\ln\frac{\sqrt C_2 r - C_1^2}{\sqrt C_2 r + C_1^2}+\frac{\omega r}{C_2}+C_3.
\theta =C_3+\frac{\omega r}{C_2} - \frac{1}{\sqrt C_2}\left(1+\frac{\omega C_1^2}{C_2}\right)\text{artanh}\left(\frac{\sqrt C_2}{C_1^2}r^2\right)
And sooo we are going to find C_1, C_2, and C_3.
For C_1 we need to use r(0)=R and r\dot\theta(0)=v_0\cos\alpha.
R=\frac{C_1}{\displaystyle \sqrt{\omega + \frac{v_0\cos\alpha}{R}}}\quad\Rightarrow\quad C_1 = R\displaystyle \sqrt{\omega + \frac{v_0\cos\alpha}{R}}.
For C_2 we should use \dot r(0) =-v_0\sin\alpha:
\dot r^2(0) = -\frac{C_1^4}{R^2}+C_2\quad\Rightarrow\quad C_2 = v_0^2\sin^2\alpha+(\omega R+v_0\cos\alpha)^2 = v_0^2+\omega^2R^2+2v_0\omega R\cos\alpha.
For C_3 we use \theta(0)=0:
C_3 = \frac{1}{\sqrt C_2}\left(1+\frac{\omega C_1^2}{C_2}\right)\text{artanh}\left(\frac{\sqrt C_2}{C_1^2}R^2\right)-\frac{\omega R}{C_2},
So the \theta(r) relation is
\theta = \frac{1+\omega C_1^2/C_2}{\sqrt C_2}\text{artanh}\left(\frac{C_1^2\sqrt C_2(R^2-r^2)}{C_1^4-C_2R^2r^2}\right)-\frac{\omega(R-r)}{C_2}.
What here is wrong is that for r=R there is only one solution for \theta (equals 0, which is obvious). Seems like I should solve everything again from scratch
4 лайка
This was in a mock test and the time given for solving this was 30 minutes. And… there was an asterisk indicating this was too much lol
@Ersultan wanna give it a try??
Maybe relax… and try someother day if you want to… you have given it soo much 
efforts. Hats off to your dedication. Clear difference between a medalist and someone who is not a medalist (me).
1 лайк
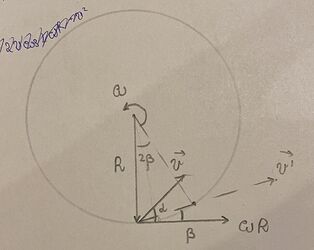
For the first part you can consider the uniform motion of the ball to be along the line of with \vec v' = \vec v + \vec \omega \times \vec R. The distance at which ball falls from the batsman will be equal to the arc distance between intesection points of this line with cylinder minus the distance traveled by the batsman due to rotation.
For the figure above we can write the following equations:
\tan(\beta) = \frac{v \sin(\alpha)}{\omega R \pm v \cos(\alpha)}
l= 2R \left(\beta - \frac{\omega R \sin(\beta)}{\sqrt{(\omega R \pm v \cos(\alpha))^2 + v^2 \sin(\alpha)^2}} \right)
Calculating this for \pm signs you will get 108 and 132 meters.
Second part is really messy and probably can be solved geometrically in lab frame by finding positions of batsman and the ball.
5 лайков