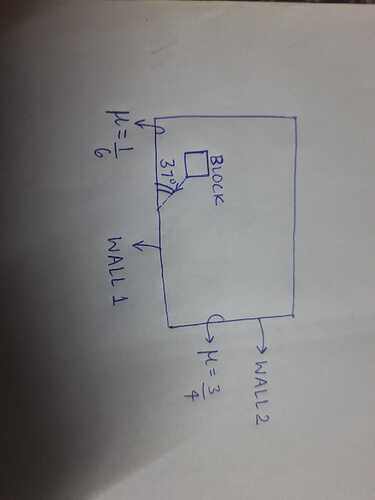
Показан вид сверху на четыре стены комнаты. Пол комнаты гладкий, но стены шероховатые, и показан их коэффициент трения. Блок, движущийся по полу со скоростью 10 м/с, сначала ударяется о стену 1, а затем о стену 2. Какова скорость блока после удара о стену 2?
do you know how to calculate block’s reflection angle?
1 лайк
I have tried but I am not getting it… I struggle with these problems, could you please explain the process or solution? There is top view so never attempted problem with top view given
just show me your attempt to solve this problem, i’ll give you a hint
1 лайк
Ok. My approach is that since top view is given then the gravity force will be perpendicular to frame, now assuming there is a frictional force at wall 1 and then I thought of momentum change parallel to wall face and tried to calculate it but got stuck… don’t know how to proceed? How will it strike and in top view I have never solved before.
This is my first time dealing with a cube in 3D with walls and floors… I have solved using balls or spherical shapes which are in 2D collision.
and so we do not need to consider it because the floor is smooth
while being in contact with the wall, the \mu N friction force changes the momentum. An overall change in momentum is \mu \int Ndt, whilst the integral \int Ndt can be found through change of momentum in perpendicular-to-the-wall projection
1 лайк
Ok i am trying using this approach… but i did not get the perpendicular to wall projection part… how do we visualise the collision??
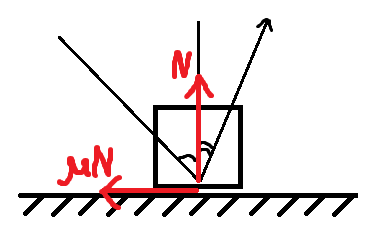
Using n and \tau to denote normal and tangential projections and v_0=10 \space\text{m/s}, the perpendicular projection of velocity is v_0^n=v_0\sin37 and apparently after collision it has become v_1^n=-v_0^n (i assume that the collision is elastic, but i’m not sure whether it is allowed or not). Thus the change of momentum is
\int N dt = m(v_0^n-v_1^n) = 2mv_0\sin37.
Then you do the same thing with the change of momentum in tangential projection and therefore calculate the reflection angle
1 лайк
Ok , I am trying to find reflection angle right now…
I am getting reflection angle as tan(θ) = 0.20 is this correct??
Sorry, I almost forgot that elastic collision implies that the speed of the block hasn’t changed, so v_1^n\neq-v_0^n but (v_1^n)^2+(v_1^\tau)^2=v_0^2 (because conservation of energy demands so).
1 лайк
oh… now I have got a bit confused…
it simply means that v_1^n=v_0\sin\alpha and v_1^\tau=v_0\cos\alpha, so you use above two equations from momentum conservation and find \alpha
Alright… I’ll try again, hopefully I get it right this time
I am getting tan(θ) = 0.4202
well, i’ve got \alpha=55.92\degree. note that \arctan 0.4202=22.79\degree, but it is obvious that \alpha should be greater than 37\degree
ohh then I have made a mistake…
I am not getting anywhere… I will again give it try sometime after… how do you get 55 degrees??
1 лайк
so in tangential projection I have
\mu \int Ndt = mv_0(\cos 37 - \cos\alpha) = \mu\cdot mv_0(\sin37 + \sin \alpha) \Rightarrow\\ \cos\alpha+\mu\sin\alpha = \cos37-\mu\sin37.
Here I could use \cos\alpha = \sqrt{1-\sin^2\alpha} and solve quadratic equation, but just rearranging it in canonic form (ax^2+bx+c=0) is too time-consuming. Instead of that, using \cos(\alpha-\beta)=\cos\alpha\cos\beta + \sin\alpha\sin\beta, I can write
\cos\alpha+\mu\sin\alpha=\sqrt{1+\mu^2}\left(\frac{1}{\sqrt{1+\mu^2}}\cos\alpha + \frac{\mu}{\sqrt{1+\mu^2}}\sin\alpha\right) = \sqrt{1+\mu^2}\cos(\alpha-\arctan\mu),
thus
\alpha =\arccos\frac{\cos37-\mu\sin37}{ \sqrt{1+\mu^2}} + \arctan\mu = 55.92\degree.
3 лайка