1 лайк
Рассмотрим малые колебания идеального газа в цилиндре:
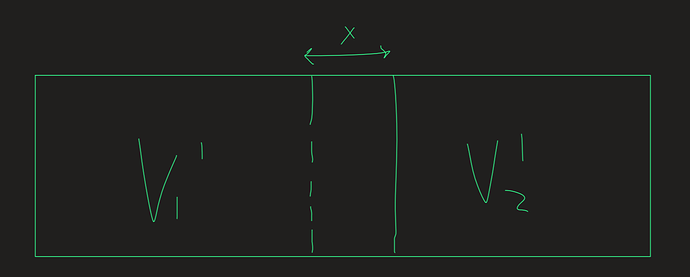
В состоянии равновесия в обеих частях цилиндра одинаковый объем газа: (V_1=V_2=V_0)
Теперь допустим, что поршень двинулся на малое расстояние x вправо:
Изменение объема \Delta V можно выразить так:
\Delta V=Sx
Объемы V_1',V_2', после перемещения поршня:
V_1'=V1+\Delta V=V_0+\Delta V=V_0+Sx
V_2'=V2-\Delta V=V_0-\Delta V= V_0 - Sx
Учитывая малость перемещения x<<\frac{V_0}{S}, воспользуемся первым приближением:
(1+x)^n\approx1+nx, |x|<<1
V1'^\gamma=(V_0+Sx)^\gamma=V_0(1+\frac{Sx}{V_0})^\gamma\approx V_0(1+\frac{\gamma Sx}{V_0})
V_2'^\gamma=(V_0-Sx)^\gamma=V_0(1-\frac{Sx}{V_0})^\gamma\approx V_0(1-\frac{\gamma Sx}{V_0})
А окончательный результат выходит так:
p_1'V_1'^\gamma=p_2'V_2'^\gamma \longrightarrow p_1'V_0(1+\frac{\gamma Sx}{V_0})=p_2'V_0(1-\frac{\gamma Sx}{V_0})
p_2'=p_1'\frac{(1+\frac{\gamma Sx}{V_0})}{(1-\frac{\gamma Sx}{V_0})} \longrightarrow p_2'\approx p_1'(1+\frac{\gamma Sx}{V_0})^2\approx p_1'(1+\frac{2\gamma Sx}{V_0})
Здесь тоже были использованы приближения:
\frac{1}{(1-\frac{\gamma Sx}{V_0})}=(1-\frac{\gamma Sx}{V_0})^{-1}\approx(1+\frac{\gamma Sx}{V_0})
(1+\frac{\gamma Sx}{V_0})^2\approx(1+\frac{2\gamma Sx}{V_0})
Отсюда находим разность давлений:
\Delta p=p_2'-p_1'=p_1'(\frac{2\gamma Sx}{V_0})
Здесь также нужно воспользоваться приближением за счет малости колебаний:
p_1'\approx p_0\longrightarrow \Delta p\approx p_0(\frac{2\gamma Sx}{V_0})
Дальше 2-ЗН:
m\ddot{x}=-\Delta pS\longrightarrow \ddot x +(p_0(\frac{2\gamma S^2x}{V_0}))x=0, \ddot
x+\omega^2x=0
\omega=\sqrt{p_0(\frac{2\gamma S^2x}{V_0})}
Проверь размерности
Здесь было использовано уравнение для адиабатического процесса:
pV^\gamma=const
7 лайков
Да я знал что тут уравнение адиабатп используется, но не понял то приближение со степенью, спасибо за блестящее объяснение
1 лайк